Courbes planes paramétrées
Dans ce qui suit,
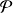 désigne le plan affine euclidien rapporté à un repère orthonormal
désigne le plan affine euclidien rapporté à un repère orthonormal
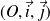 et
et
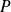 le plan vectoriel associé.
le plan vectoriel associé.
Définition :
Un arc paramétré
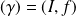 de classe
de classe
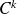 est un couple formé d'un intervalle
est un couple formé d'un intervalle
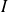 de
de
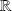 d'intérieur non vide et d'une application
d'intérieur non vide et d'une application
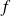 de classe
de classe
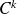 de
de
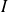 dans
dans
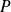 .
.
Pour tout
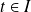 , on note
, on note
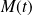 le point de
le point de
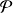 défini par :
défini par :
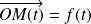 .
.
Le support de l'arc paramétré est :
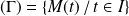 et
et
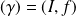 est un paramétrage de
est un paramétrage de
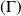 .
.
Le paramétrage donne la façon dont le support
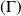 est décrit.
est décrit.
En particulier, la trajectoire d'un point matériel est un arc paramétré : à tout instant
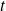 d'un intervalle
d'un intervalle
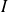 , on associe la position
, on associe la position
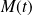 du point.
du point.
Définition :
Changement de paramétrage
Si
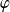 est un
est un
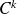 - difféomorphisme de
- difféomorphisme de
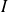 dans un intervalle
dans un intervalle
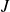 de
de
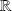 , alors
, alors
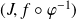 est un autre paramétrage de
est un autre paramétrage de
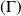 .
.
Deux paramétrages sont de même sens si l'application
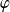 est strictement croissante. Sinon, ils sont de sens contraires.
est strictement croissante. Sinon, ils sont de sens contraires.
On définit ainsi deux classes d'équivalence. L'arc est orienté lorsque l'on a choisi un paramétrage, donc l'une des deux classes.
Définition :
Soit
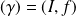 un arc paramétré de classe
un arc paramétré de classe
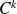 avec
avec
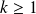 .
.
Le vecteur vitesse à l'instant
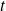 est défini par :
est défini par :
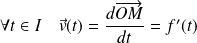 .
.
Un point
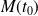 de
de
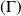 est régulier si :
est régulier si :
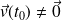 . Sinon, le point est stationnaire.
. Sinon, le point est stationnaire.
La notion de régularité est indépendante du paramétrage choisi : c'est une notion géométrique.
Un arc paramétré
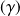 est régulier si tous les points de
est régulier si tous les points de
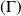 sont réguliers.
sont réguliers.
Définition :
Soit
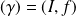 un arc paramétré de classe
un arc paramétré de classe
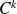 avec
avec
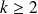 .
.
Le vecteur accélération à l'instant
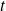 est défini par :
est défini par :
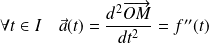 .
.
Un point
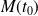 de
de
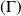 est birégulier si
est birégulier si
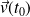 et
et
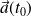 ne sont pas colinéaires.
ne sont pas colinéaires.
La notion de birégularité est aussi une notion géométrique.
Un arc paramétré est birégulier si tous les points de
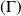 sont biréguliers.
sont biréguliers.
Fondamental :
Soit
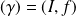 un arc paramétré de classe
un arc paramétré de classe
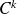 avec
avec
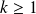 et
et
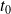 un point de
un point de
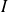 où l'une au moins des dérivées successives de
où l'une au moins des dérivées successives de
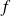 n'est pas nulle.
n'est pas nulle.
Soit
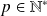 le plus petit entier pour lequel la dérivée d'ordre
le plus petit entier pour lequel la dérivée d'ordre
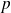 de
de
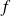 ne s'annule pas en
ne s'annule pas en
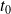 .
.
Alors la courbe
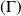 admet en
admet en
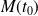 une tangente de vecteur directeur
une tangente de vecteur directeur
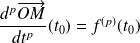 .
.
Si
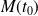 est un point régulier,
est un point régulier,
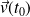 est un vecteur directeur de la tangente à
est un vecteur directeur de la tangente à
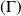 .
.
Sous réserve d'existence, la tangente à
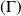 en
en
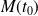 est la position limite de la sécante
est la position limite de la sécante
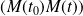 quand
quand
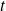 tend vers
tend vers
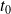 .
.
Définition :
Sur le support
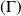 d'un arc paramétré
d'un arc paramétré
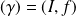 de classe
de classe
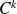 avec
avec
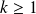 , on choisit une origine
, on choisit une origine
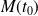 .
.
L'abscisse curviligne d'un point
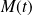 est :
est :
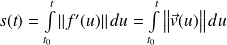 .
.
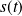 représente la "distance parcourue" le long de
représente la "distance parcourue" le long de
 entre
entre
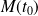 et
et
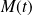 .
.
Si
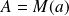 et
et
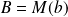 où
où
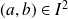 , la "longueur" de l'arc
, la "longueur" de l'arc
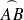 est :
est :
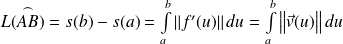 .
.
Fondamental :
Propriétés
Si l'arc est régulier,
 est un
est un
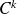 - difféomorphisme de
- difféomorphisme de
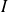 dans
dans
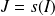 , et
, et
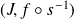 est un paramétrage de
est un paramétrage de
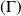 .
. Le vecteur tangent
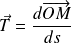 est un vecteur unitaire.
est un vecteur unitaire.
On obtient donc un nouveau paramétrage de la courbe appelé paramétrage normal.
Définition :
Soit
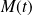 un point birégulier de la courbe
un point birégulier de la courbe
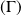 .
.
On appelle repère de Frenet au point
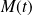 le repère orthonormé direct
le repère orthonormé direct
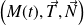 où
où
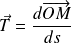 .
.
Soit
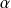 une mesure de l'angle
une mesure de l'angle
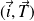 . Donc :
. Donc :
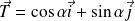 et
et
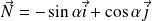 .
.
La courbure de la courbe au point
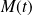 est :
est :
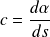 .
.
Le rayon de courbure est le réel :
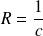 .
.
Le centre de courbure est le point
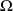 tel que
tel que
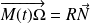 .
.
Le cercle osculateur est le cercle de centre
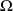 et de rayon
et de rayon
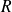 .
.
La normale au point
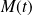 à la courbe
à la courbe
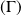 est la droite passant par
est la droite passant par
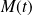 et de vecteur directeur
et de vecteur directeur
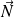 .
.
Le centre de courbure est sur la normale à la courbe.
Le cercle osculateur est le cercle qui "épouse le mieux" la forme de la courbe au voisinage du point.
Fondamental :
Formules de Frenet
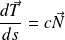 , et
, et
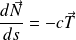 .
. 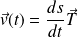 , et
, et
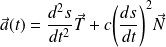 .
.





