Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Un vélo roule (sans glisser) sur une route.
On se propose d'étudier la courbe décrite par la valve de l'une de ses roues. On choisit comme origine un instant où la valve se trouve au point de tangence avec la route, et on limite l'étude à l'instant où la valve est revenue au point de tangence avec la route.
La courbe se reproduit ensuite par translation. Une telle courbe s'appelle une cycloïde.
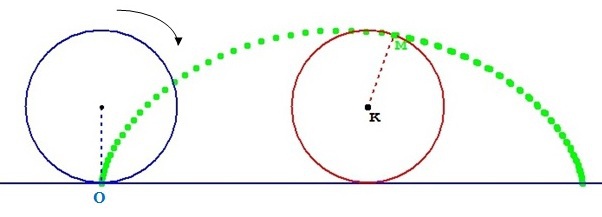
Le problème revient donc à étudier dans le plan affine euclidien le lieu
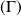d'un point
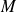d'un cercle de rayon
qui roule sans glisser sur une droite
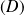. On oriente la droite
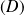dans le sens du déplacement par son vecteur unitaire
.
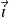Soit
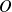le point de tangence à l'instant
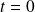, et
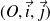un repère orthonormé direct. A l'instant
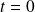, le point
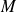est en
.
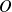Question
Déterminer les coordonnées du point
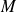à l'instant
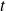de l'intervalle
.
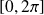Soit
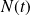le point de tangence du cercle avec la droite à l'instant
.
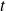La distance parcourue par le centre du cercle est égale à la longueur de l'arc de cercle
.
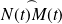A l'instant
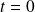, le centre du cercle est le point
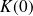de coordonnées
.
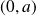Et le point
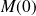a pour coordonnées
.
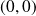A l'instant
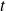, le centre du cercle est le point
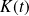de coordonnées
.
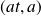Le nouveau point de tangence est
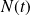de coordonnées
.
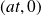La distance
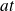parcourue par le centre du cercle est égale à la longueur de l'arc de cercle
.
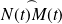Donc l'angle
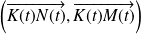a pour mesure
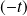ou
.
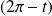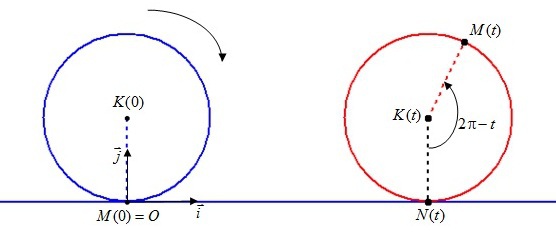
Donc l'angle
a pour mesure
.
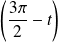Donc :
.
Conclusion : Le point
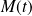a pour coordonnées
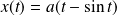et
.
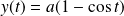Question
Montrer que la courbe
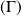admet en tous ses points une tangente.
Pour chaque point, déterminez la première dérivée non nulle.
Soit
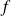la fonction vectorielle définie sur l'intervalle
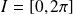par :
.
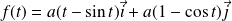La courbe
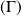est le support de l'arc paramétré
.
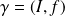La fonction
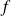est de classe
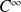sur
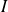et :
.
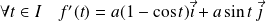Donc :
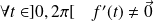, donc
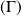admet en
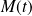une tangente de vecteur directeur :
.
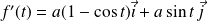Et :
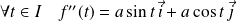. Donc :
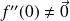et
.
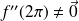Donc
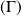admet en
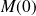et
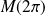une tangente de vecteur directeur
.
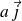Conclusion : La courbe
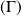admet en tous ses points une tangente.
Aux points
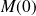et
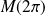, la tangente est verticale.
Question
Calculer la longueur de l'arche de cycloïde parcourue par le point
.
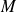Déterminez l'abscisse curviligne du point
.
.
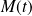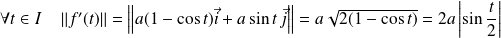Or :
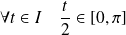, donc
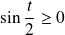. Donc :
.
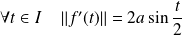On choisit pour origine sur
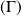le point
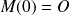et on note
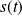l'abscisse curviligne du point
.
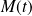Donc :
.
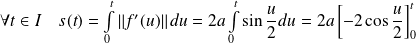Donc l'abscisse curviligne du point
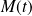est :
.
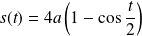La longueur de l'arche de cycloïde est :
.
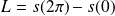Conclusion : La longueur de l'arche de cycloïde est :
.
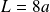Question
Déterminer le rayon de courbure et le centre de courbure de
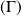au point
.
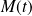Déterminez l'angle
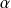de
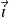avec le vecteur tangent
.
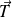D'après les calculs précédents :
.
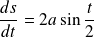Donc :
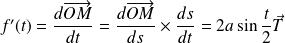et
.
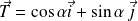Or :
.
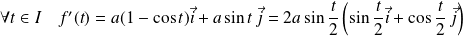Donc :
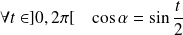et
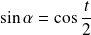, et donc :
.
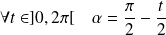Or :
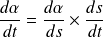, donc la courbure au point
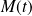est :
.
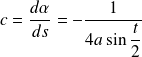Conclusion : Le rayon de courbure au point
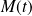est :
.
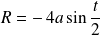Le vecteur normal du repère de Frenet est :
.
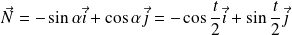Et le centre de courbure est le point
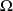défini par :
.
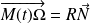Donc :
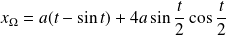, et :
.
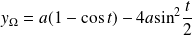Conclusion : Le centre de courbure
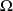a pour coordonnées
.
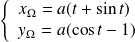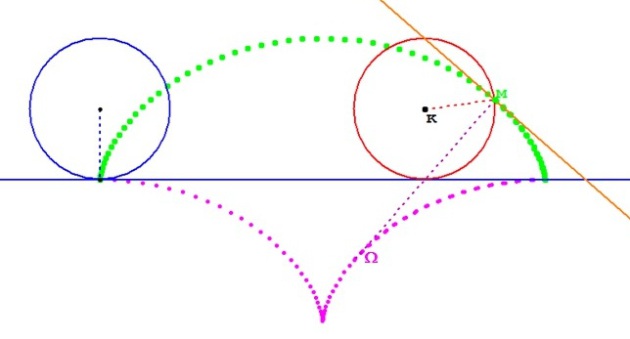
Le centre de courbure
décrit une autre cycloïde.
