Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
En posant :
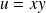et
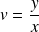, déterminer les fonctions
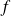de classe
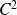sur
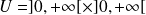qui vérifient :
.
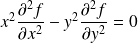Montrez que l'application
:
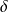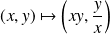est un difféomorphisme et introduisez la fonction
.
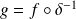L'application
:
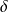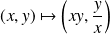est définie et de classe
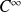sur
.
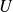Son jacobien :
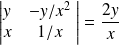est non nul sur
.
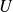Sur
:
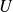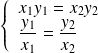implique :
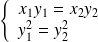, donc :
.
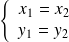Donc l'application
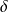est injective sur l'ouvert
.
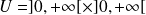Donc d'après le théorème d'inversion, l'application
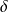est un
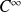- difféomorphisme de
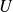dans l'ouvert
.
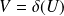La fonction
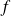est de classe
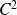sur
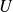si et seulement si la fonction
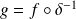est de classe
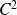sur
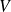car
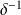est de classe
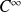de
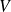dans
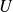. Et :
.
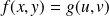Donc :
.
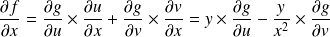Donc :
.
.
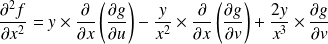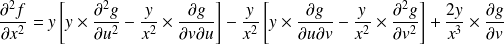Donc :
.
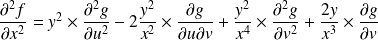Et :
.
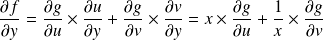Donc :
.
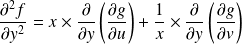Donc :
.
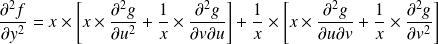Donc :
.
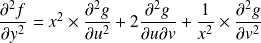Donc l'équation
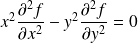équivaut à :
.
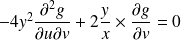Donc la fonction
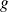est solution de l'équation :
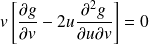. Or :
.
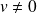Donc, pour tout
, la fonction
:
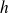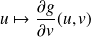vérifie :
.
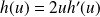Donc il existe une fonction
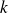telle que :
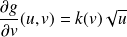. On intègre par rapport à
.
Donc il existe deux fonctions
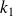et
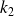telles que :
.
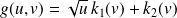Donc :
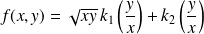. Or :
.
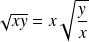Donc il existe deux fonctions
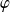et
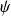telles que :
.
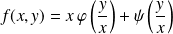Or la fonction
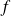est de classe
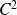sur
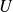, donc les fonctions
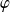et
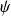sont de classe
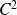sur
.
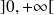Réciproquement, si
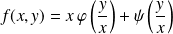où
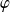et
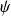sont des fonctions de classe
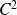sur
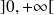, alors
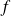est de classe
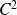sur
.
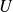Alors :
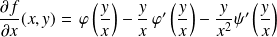, et :
.
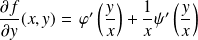Donc :
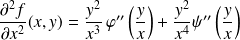, et :
.
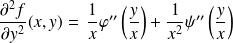Donc :
.
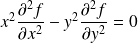Donc la fonction
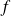est solution de l'équation.
Conclusion : Une fonction
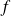est solution sur
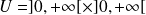de l'équation
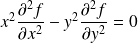si et seulement si il existe des fonctions
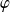et
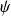de classe
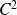sur
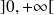telles que :
.
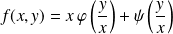