Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
A quelle condition sur les réels
,
,
et
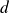, l'application
:
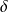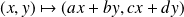est-elle un difféomorphisme de
dans lui-même ?
Utilisez la définition d'un difféomorphisme.
L'application
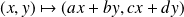est linéaire et de classe
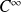sur
.
Sa matrice est :
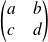, donc elle est bijective si et seulement si
.
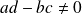Alors, sa réciproque est :
.
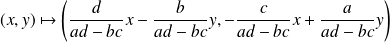Elle est aussi de classe
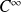sur
.
Conclusion : L'application
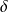est un
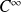- difféomorphisme de
dans lui-même si et seulement si
.
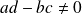On suppose cette condition réalisée, et pour toute fonction
de classe
ou
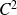sur
, on définit la fonction
.
Question
Exprimer les dérivées partielles d'ordre
et
de
par rapport à
et à
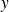en fonction des dérivées partielles de
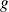par rapport à
et à
.
Il s'agit de dériver des fonctions composées.
La fonction
est de même classe que
sur
car
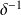est de classe
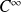sur
.
Et :
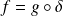, donc :
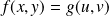en posant
et
.
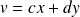Donc :
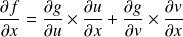, et :
.
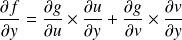Conclusion :
, et
.
.
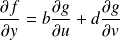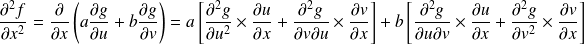Conclusion :
.
.
Conclusion :
.
.
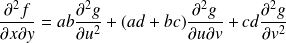Conclusion :
.
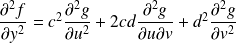Question
Déterminer toutes les fonctions
de classe
sur
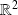qui vérifient :
.
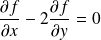Effectuez un changement de variable de la forme
et
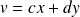pour simplifier l'équation.
On pose :
et
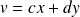, et on définit la fonction
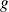par :
.
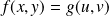La fonction
est de classe
sur
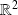si et seulement si la fonction
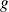est de classe
sur
.
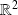L'équation
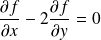équivaut à :
.
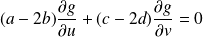Donc si
ou
(avec
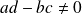), on a un seul terme.
Par exemple, par changement de variable
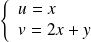, on obtient :
.
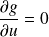Donc il existe une fonction
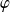telle que :
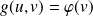, donc telle que :
.
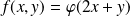Or la fonction
est de classe
sur
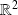, donc la fonction
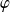est de classe
sur
.
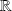Réciproquement, si
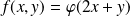où
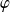est une fonction de classe
sur
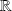, alors la fonction
est de classe
sur
.
Alors :
et
, donc :
.
Donc 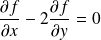la fonction
est solution de l'équation.
Conclusion : Une fonction
est solution de l'équation
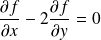sur
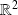si et seulement si il existe une fonction
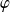de classe
sur
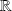telle que :
.
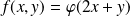Question
Déterminer toutes les fonctions
de classe
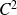sur
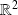qui vérifient :
.
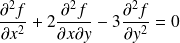Effectuez un changement de variable de la forme
et
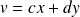pour simplifier l'équation.
On pose :
et
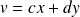, et on définit la fonction
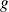par :
.
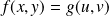La fonction
est de classe
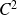sur
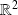si et seulement si la fonction
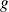est de classe
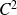sur
.
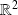L'équation
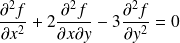équivaut à :
.
L'équation devient plus simple si deux des coefficients sont nuls car on n'obtient plus qu'un seul terme.
Or l'équation :
a pour racines
et
.
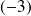Donc, si
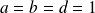et
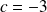, on a :
.
Donc par changement de variable
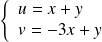, on obtient :
.
Donc il existe une fonction
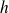telle que :
.
Cette fonction
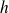est de classe
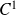car
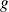est de classe
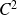, donc elle admet une primitive
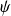qui est de classe
.
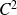Donc il existe deux fonctions
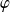et
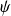telles que :
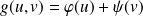, donc telles que :
.
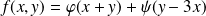Or, la fonction
est de classe
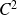sur
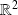, donc les fonctions
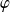et
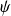sont de classe
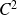sur
.
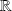Réciproquement, si
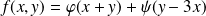où
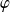et
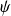sont des fonctions de classe
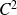sur
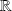, alors la fonction
est de classe
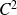sur
.
Alors :
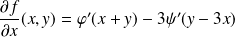, et :
.
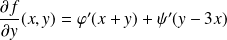Donc les dérivées partielles d'ordre
sont :
.
.
.
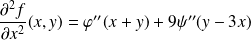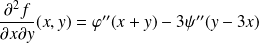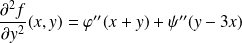Donc :
.
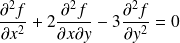Donc la fonction
est solution de l'équation.
Conclusion : Une fonction
est solution de l'équation
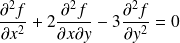sur
si et seulement si il existe deux fonctions
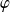et
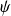de classe
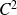sur
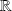telles que :
.
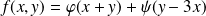Question
Déterminer toutes les fonctions
de classe
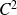sur
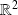qui vérifient :
.
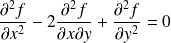Effectuez un changement de variable de la forme
et
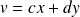pour simplifier l'équation.
On pose :
et
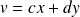, et on définit la fonction
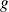par :
.
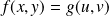La fonction
est de classe
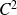sur
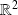si et seulement si la fonction
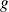est de classe
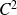sur
.
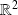L'équation
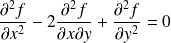équivaut à :
.
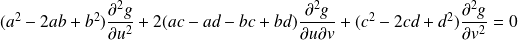On cherche aussi à rendre deux des coefficients nuls pour avoir un seul terme.
Or l'équation :
n'a qu'une racine
, donc on ne peut pas annuler le premier et le troisième avec
.
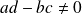On choisit
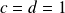pour annuler le troisième. Alors le deuxième coefficient est aussi nul.
On peut par exemple choisir :
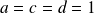et
.
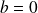Donc par changement de variable
, on obtient :
.
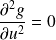Donc il existe une fonction
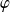telle que :
.
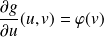Donc il existe deux fonctions
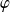et
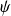telles que :
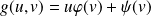, donc telles que :
.
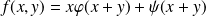Or, la fonction
est de classe
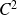sur
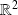, donc les fonctions
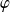et
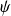sont de classe
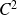sur
.
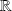Réciproquement, si
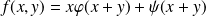où
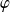et
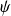sont des fonctions de classe
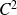sur
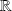, alors la fonction
est de classe
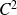sur
.
Alors :
, et :
.
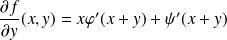Donc les dérivées partielles d'ordre
sont :
.
.
.
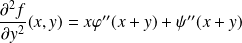Donc :
.
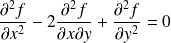Donc la fonction
est solution de l'équation.
Conclusion : Une fonction
est solution de l'équation
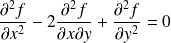sur
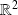si et seulement si il existe des fonctions
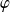et
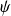de classe
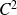sur
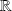telles que :
.
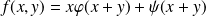