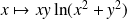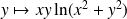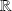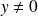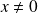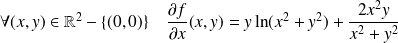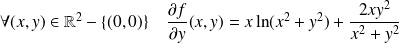Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
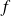la fonction définie par :
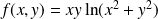si
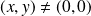et
.
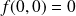Question
Montrer que la fonction
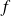est continue sur
.
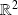Sur
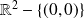, utilisez les opérations sur les fonctions continues.
En
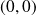, utilisez une majoration de la fonction.
La fonction
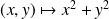est continue et strictement positive sur
.
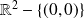Donc par composition, la fonction
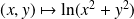est continue sur
.
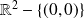Et les fonctions
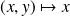et
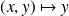sont continues sur
.
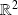Donc la fonction
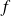est continue sur
.
.
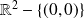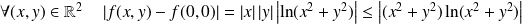Or :
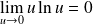. Donc :
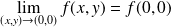. Donc
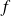est continue en
.
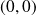Conclusion : La fonction
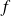est continue sur
.
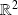Question
Question
Montrer que
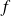admet des dérivées partielles en
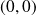et les calculer.
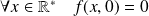et
.
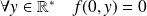Donc :
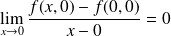et :
.
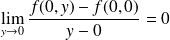Conclusion : La fonction
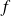admet des dérivées partielles nulles par rapport à
et à
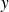en
.
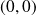Question
La fonction
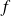est-elle différentiable sur
?
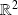Etudiez la continuité des dérivées partielles.
Par composition et opérations algébriques, les dérivées partielles de
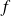par rapport à
et par rapport à
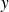sont continues sur
.
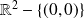Etudions la continuité en
.
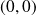Or :
.
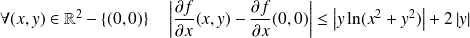Donc :
.
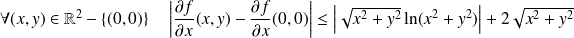Or :
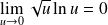. Donc :
.
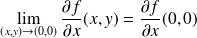De même :
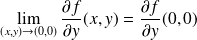par symétrie des deux expressions.
Donc les dérivées partielles sont continues en
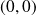, donc sur
.
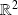Conclusion : La fonction
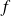est différentiable sur
.
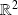Remarque :
De plus, on pourra en déduire que la fonction
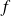est de classe
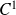sur
.
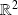