Dérivées partielles d'ordre 1
Dans ce qui suit,
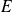 et
et
 sont des
sont des
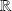 - espaces vectoriels normés de dimension finie,
- espaces vectoriels normés de dimension finie,
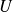 est un ouvert non vide de
est un ouvert non vide de
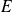 et
et
 est une application de
est une application de
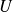 dans
dans
 .
.
Définition :
La fonction
 admet une dérivée en
admet une dérivée en
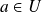 suivant le vecteur
suivant le vecteur
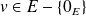 si la fonction
si la fonction
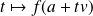 est dérivable en
est dérivable en
 .
.
La dérivée de
 en
en
 suivant le vecteur
suivant le vecteur
 est la fonction définie par :
est la fonction définie par :
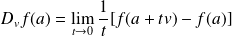 .
.
Exemple : Soit
 la fonction définie par
la fonction définie par
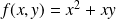 .
.
Il s'agit d'une application de
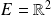 dans
dans
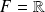 .
.
Soit
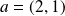 et
et
 un vecteur non nul.
un vecteur non nul.
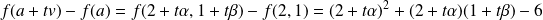 .
.
Donc :
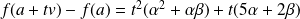 .
.
Donc
 admet en
admet en
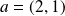 une dérivée suivant
une dérivée suivant
 :
:
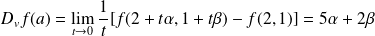 .
.
Fondamental :
Propriétés
Si
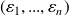 est une base de
est une base de
 ,
,
 est dérivable en
est dérivable en
 suivant
suivant
 si et seulement si toutes ses coordonnées
si et seulement si toutes ses coordonnées
 le sont. Alors :
le sont. Alors :
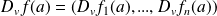 .
.Si
 est différentiable en
est différentiable en
 , alors
, alors
 admet en
admet en
 une dérivée suivant tous les vecteurs
une dérivée suivant tous les vecteurs
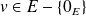 . Et :
. Et :
 .
.
Dans l'exemple précédent, la fonction
 est différentiable en
est différentiable en
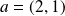 .
.
En effet, si
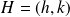 :
:
 .
.
Donc :
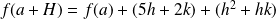 .
.
L'application
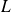 :
:
 est linéaire et :
est linéaire et :
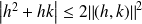 , donc :
, donc :
 .
.
Donc la fonction
 est différentiable en
est différentiable en
 et
et
 est l'application :
est l'application :
 .
.
Donc, pour tout vecteur
 non nul :
non nul :
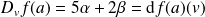 .
.
Définition :
Si
 est une base de
est une base de
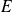 ,
,
 admet une dérivée partielle en
admet une dérivée partielle en
 par rapport à
par rapport à
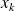 si
si
 admet une dérivée en
admet une dérivée en
 suivant le vecteur
suivant le vecteur
 .
.
La dérivée partielle de
 en
en
 par rapport à
par rapport à
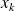 est la fonction définie par :
est la fonction définie par :
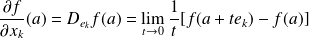 .
.
Dans l'exemple précédent, la base canonique de
 est :
est :
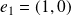 et
et
 .
.
Donc :
 . Donc :
. Donc :
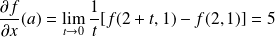 .
.
Et :
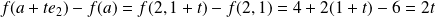 . Donc :
. Donc :
 .
.
La fonction
 admet en
admet en
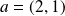 des dérivées partielles d'ordre
des dérivées partielles d'ordre
 par rapport à
par rapport à
 et par rapport à
et par rapport à
 :
:
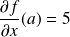 et
et
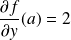 .
.
Méthode :
Dans la pratique, pour calculer la dérivée partielle de
 par rapport à une variable
par rapport à une variable
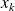 en
en
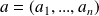 , on considère toutes les autres variables comme des paramètres constants, et on dérive la fonction
, on considère toutes les autres variables comme des paramètres constants, et on dérive la fonction
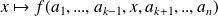 en
en
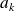 .
.
Dans l'exemple précédent, la dérivée partielle par rapport à
 est la dérivée de la fonction
est la dérivée de la fonction
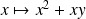 .
.
Donc :
 . Donc :
. Donc :
 .
.
De même, la dérivée partielle par rapport à
 est la dérivée de la fonction
est la dérivée de la fonction
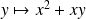 .
.
Donc :
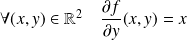 . Donc :
. Donc :
 .
.
Fondamental :
Propriétés
Si
 est différentiable en
est différentiable en
 , alors
, alors
 admet des dérivées partielles d'ordre
admet des dérivées partielles d'ordre
 et :
et :
 .
.Si
 admet des dérivées partielles continues en
admet des dérivées partielles continues en
 , alors
, alors
 est différentiable en
est différentiable en
 .
.
Attention :
Attention ! Une fonction peut admettre des dérivées partielles en
 sans être différentiable.
sans être différentiable.





