Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les deux questions suivantes sont indépendantes.
Soit
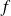 la fonction définie par :
la fonction définie par :
 si
si
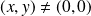 et
et
 .
.
Question
Etudier l'existence de dérivées partielles d'ordre
 de la fonction
de la fonction
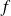 .
.
Etudiez d'abord l'existence des dérivées partielles sur
 , puis en
, puis en
 .
.
On a :
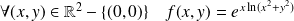 .
.
La fonction
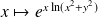 est dérivable sur
est dérivable sur
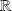 si
si
 et sur
et sur
 si
si
 .
.
Donc
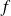 admet une dérivée partielle par rapport à
admet une dérivée partielle par rapport à
 sur
sur
 .
.
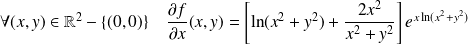 .
.
La fonction
 est dérivable sur
est dérivable sur
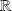 .
.
Donc
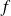 admet une dérivée partielle par rapport à
admet une dérivée partielle par rapport à
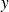 sur
sur
 .
.
Et :
 .
.
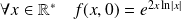 . Donc :
. Donc :
 car :
car :
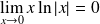 .
.
Donc le quotient
 n'a pas de limite réelle en
n'a pas de limite réelle en
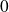 .
.
Donc
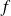 n'admet pas de dérivée partielle par rapport à
n'admet pas de dérivée partielle par rapport à
 en
en
 .
.
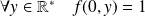 . Donc :
. Donc :
 .
.
Donc
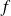 admet une dérivée partielle par rapport à
admet une dérivée partielle par rapport à
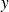 en
en
 :
:
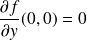 .
.
Conclusion : La fonction
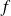 admet des dérivées partielles par rapport à
admet des dérivées partielles par rapport à
 et à
et à
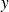 sur
sur
 . En
. En
 , elle admet seulement une dérivée partielle par rapport à
, elle admet seulement une dérivée partielle par rapport à
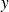 .
.
On peut d'ailleurs remarquer que la dérivée partielle de
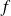 par rapport à
par rapport à
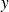 n'est pas continue en
n'est pas continue en
 car
car
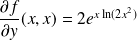 ne tend pas vers
ne tend pas vers
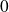 quand
quand
 tend vers
tend vers
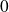 .
.
Soit
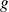 la fonction définie par :
la fonction définie par :
 si
si
 et
et
 .
.
Question
Etudier l'existence de dérivées partielles d'ordre
 de la fonction
de la fonction
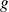 .
.
Pour chaque dérivée partielle, séparez les cas
 et
et
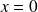 .
.
La fonction
 est dérivable sur
est dérivable sur
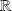 si
si
 .
.
Donc la fonction
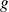 admet une dérivée partielle par rapport à
admet une dérivée partielle par rapport à
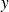 en
en
 où
où
 .
.
Et :
 si
si
 .
.
Si
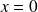 , la fonction
, la fonction
 est aussi dérivable sur
est aussi dérivable sur
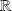 .
.
Donc la fonction
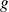 admet une dérivée partielle nulle par rapport à
admet une dérivée partielle nulle par rapport à
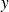 en
en
 .
.
La fonction
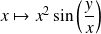 est dérivable sur
est dérivable sur
 .
.
Donc la fonction
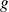 admet une dérivée partielle par rapport à
admet une dérivée partielle par rapport à
 en
en
 où
où
 .
.
Et :
 si
si
 .
.
Pour tout
 avec
avec
 :
:
 , donc :
, donc :
 .
.
Donc :
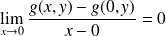 .
.
Donc la fonction
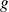 admet une dérivée partielle nulle par rapport à
admet une dérivée partielle nulle par rapport à
 en tout point
en tout point
 .
.
Conclusion : La fonction
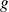 admet des dérivées partielles par rapport à
admet des dérivées partielles par rapport à
 et à
et à
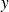 sur
sur
 .
.





