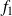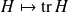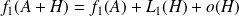Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
l'ensemble des matrices carrées d'ordre
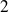à coefficients réels muni de la norme
.
Soit
l'ensemble des matrices carrées d'ordre
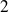inversibles à coefficients réels.
Question
Question
Montrer que l'application
:
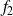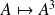est différentiable sur
et calculer sa différentielle.
Calculez
sans oublier qu'il n'y a pas commutativité.
Pour toutes matrices
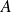et
:
.
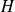Donc :
.
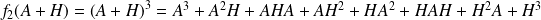L'application
:
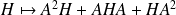est linéaire.
Et :
.
Donc :
.
Conclusion : L'application
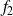est différentiable sur
.
Sa différentielle en
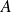est l'application
:
.
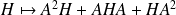Question
Montrer que l'application
:
est différentiable sur
et calculer sa différentielle.
Utilisez l'expression du déterminant d'une matrice carrée d'ordre
.
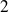Si
et
, alors :
.
Donc :
.
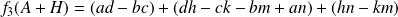L'application
:
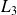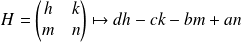est linéaire.
Et :
.
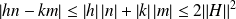Donc :
.
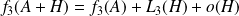Conclusion : L'application
est différentiable sur
.
Sa différentielle en
est l'application
:
.
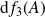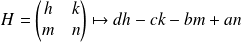Question
Montrer que l'application
:
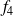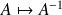est différentiable sur
et calculer sa différentielle.
Montrez d'abord que l'application
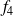est différentiable en
, puis en tout
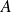de
.
L'application
:
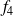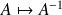est définie sur l'ensemble
des matrices inversibles.
Or l'application
:
est continue sur
, donc
est l'image réciproque d'un ouvert par une fonction continue, donc un ouvert.
Si
appartient à
, alors :
.
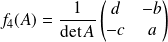Montrons d'abord que l'application est différentiable en
.
Soit
tel que
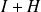appartienne à
.
.
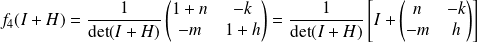Or :
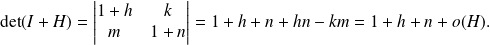
Et :
, donc :
.
Donc :
.
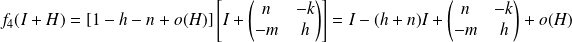Donc :
.
Donc l'application
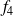est différentiable en
et
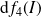est l'application :
.
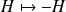Montrons maintenant qu'elle est différentiable en tout point
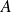de
.
Soit
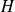tel que
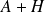appartienne à
.
.
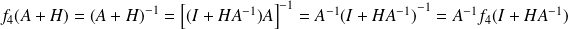Donc :
.
Or :
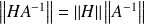. Donc :
.
Et l'application :
est linéaire.
Conclusion : L'application
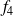est différentiable sur
.
Sa différentielle en
est l'application
:
.
