Applications différentiables
Dans ce qui suit,
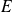et
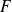sont des
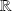- espaces vectoriels normés de dimension finie,
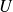est un ouvert non vide de
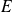et
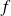est une application de
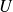dans
.
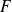Définition :
La fonction
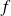admet un développement limité d'ordre
en
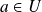s'il existe une application linéaire
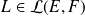et un voisinage
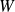de
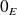tels que :
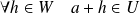et
.
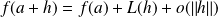Si cette application linéaire
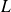existe, elle est unique.
On dira que
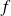est différentiable en
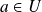et
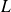est l'application linéaire tangente de
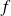en
.
Exemple : Soit
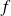la fonction définie par
.
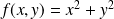Il s'agit d'une application de
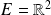dans
.
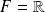Pour tout
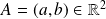et tout
:
.
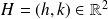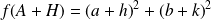Donc :
.
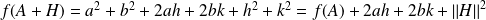L'application
:
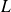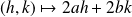est linéaire de
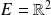dans
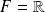. Et :
.
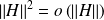Donc :
.
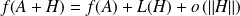Donc l'application
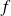est différentiable en tout point de
.
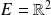Définition :
La fonction
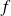est différentiable sur l'ouvert
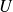si elle est différentiable en tout point de
.
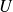Sa différentielle est l'application
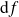de
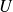dans
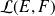qui à tout point
de
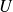associe l'application linéaire tangente de
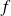en
:
.
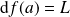Dans l'exemple précédent, la différentielle
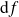est l'application qui à tout
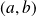de
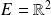associe l'application linéaire :
.
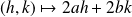Fondamental :
Propriétés
Si
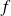est différentiable en
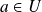, il y a unicité du développement limité d'ordre
en
.Si la fonction
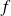est différentiable en
, alors
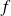est continue en
.Si
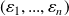est une base de
,
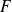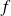est différentiable en
si et seulement si toutes ses coordonnées
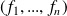le sont. Alors :
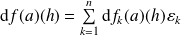.Si
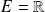, la fonction
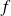est différentiable en
si et seulement si
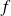est dérivable en
. Alors :
.
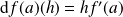Exemple : Soit
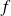la fonction définie par
.
Il s'agit d'une application de
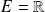dans
.
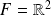Dans la base canonique, les fonctions coordonnées de
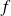sont
:
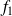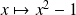et
:
.
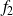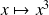Ce sont des fonctions dérivables de
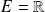dans
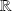, donc différentiables en tout point
.
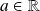Donc l'application
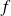est différentiable en tout point
de
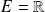et :
.
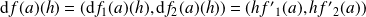Donc la différentielle
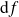est l'application qui à tout réel
associe l'application linéaire
.
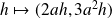Fondamental :
Opérations
Linéarité :
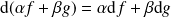.Si
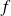est différentiable en
et si
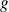est différentiable en
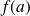, alors
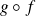est différentiable en
. Et :
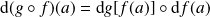.Si
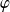est une fonction de
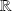dans
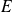dérivable en
et si
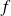est différentiable en
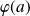, alors
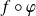est dérivable en
. Et :
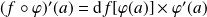.Lorsque ces opérations ont un sens et si
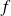et
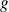sont différentiables : 
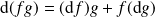(produit scalaire).
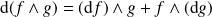(produit vectoriel).
