Exo 18
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Déterminer les solutions maximales de l'équation différentielle
:
.
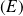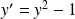Commencez par chercher les solutions constantes, puis montrez que les autres solutions ne prennent pas les valeurs
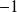et
.
Il s'agit d'une équation autonome d'ordre
.
Il y a deux solutions constantes :
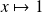et
.
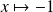La fonction
est de classe
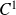sur l'ouvert
.
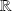Donc d'après le théorème de Cauchy-Lipschitz, pour tout réel
, il existe une unique solution maximale
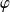qui vérifie :
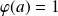. C'est donc la fonction constante
.
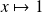De même, pour tout réel
, il existe une unique solution maximale
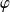qui vérifie :
. C'est la fonction constante
.
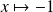Donc si
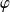une solution maximale non constante définie sur un intervalle ouvert
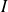, alors :
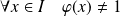et
.
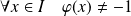L'équation
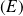est à variables séparables :
.
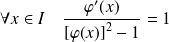Donc :
.
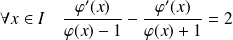Donc il existe une constante
telle que :
.
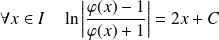Donc :
.
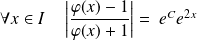Or
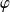est dérivable, donc continue sur
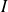, donc
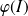est un intervalle qui ne contient ni
ni
.
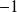Donc :
ou
ou
.
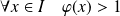Donc
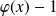et
gardent un signe constant sur
.
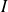Donc :
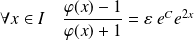avec
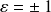. Soit :
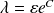, donc :
.
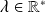Donc :
.
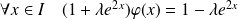Si
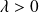, alors :
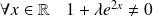, donc :
.
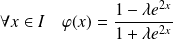Donc :
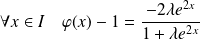et :
.
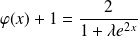Donc dans ce cas :
, donc l'intervalle maximal est
.
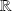Et la fonction
est bien solution de
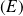sur
.
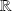Si
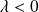, alors :
.
Il faut donc que :
ou
.
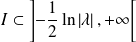Alors :
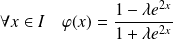, donc :
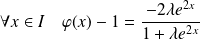et
.
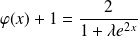Or :
, donc :
.
Et :
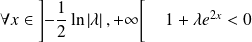, donc :
.
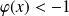Donc ces intervalles sont maximaux et la fonction
est bien solution de
.
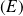Conclusion : Les solutions maximales de
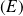sont les fonctions constantes
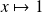et
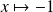, les fonctions
définies sur
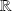pour tout réel
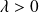, les fonctions
définies sur
ou sur
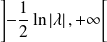pour tout réel
.
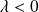