Exo 17
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
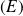l'équation différentielle :
.
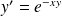Question
Justifier l'existence d'une unique solution maximale
qui vérifie :
.
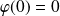Utilisez le théorème de Cauchy-Lipschitz.
Soit
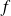la fonction définie par :
.
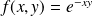La fonction
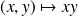est de classe
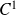sur
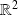et
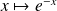est de classe
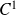sur
.
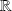Donc, par composition, la fonction
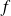est de classe
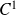sur l'ouvert
.
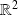On peut donc appliquer le théorème de Cauchy-Lipschitz.
Conclusion : Il existe une unique solution maximale
qui vérifie :
.
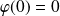Question
Démontrer que
est une fonction impaire.
Introduisez la fonction
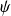définie par :
.
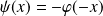La fonction
est définie sur un intervalle ouvert
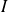contenant
.
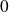Soit
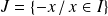et
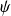la fonction définie par :
.
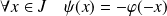Donc :
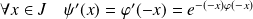car
.
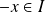Donc :
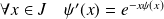et :
.
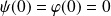Donc
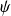est une solution de
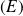qui vérifie :
.
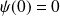Donc
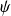est une restriction de
:
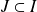et
.
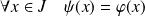Donc l'intervalle
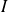est symétrique par rapport à
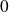et :
.
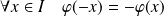Conclusion : La fonction
est impaire.
Question
Démontrer que
est définie sur
.
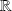Raisonnez par l'absurde.
On raisonne par l'absurde en supposant que
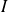est borné :
.
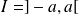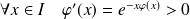, donc
est strictement croissante sur
.
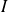Donc :
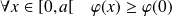, donc :
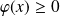, donc :
.
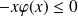Donc :
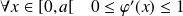, donc en intégrant :
.
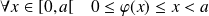Donc
est croissante et majorée sur
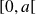, donc elle admet une limite réelle en
.
Donc
est prolongeable par continuité en
. Soit :
.
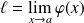Son prolongement est défini par :
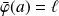et :
.
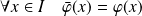Donc :
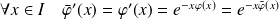et :
.
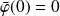De plus :
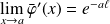. Donc
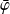est dérivable en
et :
.
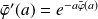Donc
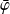est une solution de
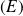sur
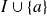, ce qui est absurde car
est maximale.
Donc l'intervalle
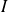n'est pas borné.
Conclusion : La fonction
est définie sur
.
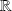Question
Démontrer que
admet une limite finie
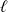en
.
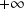Montrez que la fonction
est croissante et majorée sur
.
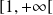La fonction
est strictement croissante sur
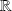car :
.
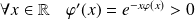Donc :
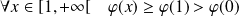, donc :
.
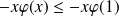Donc :
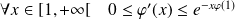et :
.
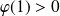Donc :
.
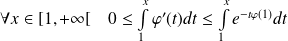Donc :
.
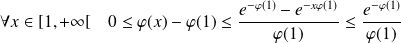La fonction
est donc croissante et majorée sur
.
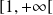Conclusion : La fonction
admet une limite finie
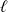en
.
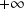Donc par parité :
.
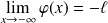Question
Démontrer que :
.
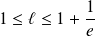Utilisez un majorant et un minorant de
pour majorer et minorer sa dérivée, puis intégrez.
La fonction
est strictement croissante, donc :
.
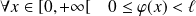Donc :
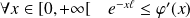. Donc :
.
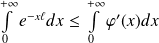Or :
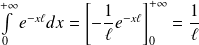et :
.
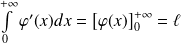Donc :
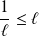. Or :
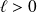. Donc :
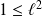, donc :
.
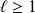La fonction
est continue et strictement croissante sur
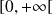et
.
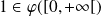Donc d'après le théorème des valeurs intermédiaires :
.
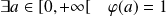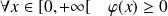, donc :
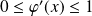, donc :
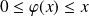, donc :
.
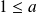Et :
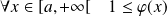, donc :
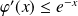, donc :
.
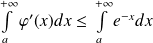Donc :
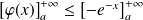. Donc :
.
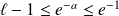Conclusion :
.
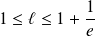Question
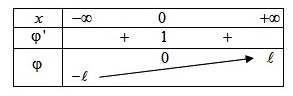
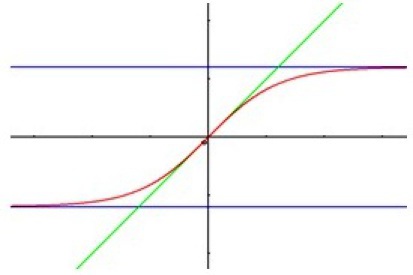
Donner le tableau de variations de
et l'allure de sa courbe représentative.
La fonction
est strictement croissante sur
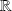et :
.
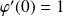