Equations différentielles non linéaires
Rappel :
Soit
un espace vectoriel normé de dimension finie,
un ouvert de
et
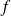une application de
dans
.
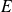Si
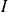est un intervalle de
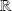d'intérieur non vide, une
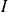-solution de l'équation différentielle
est une fonction
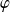dérivable sur
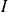qui vérifie :
.
Si
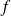est continue sur
, toute
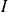-solution est de classe
sur
.
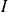Si
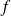est de classe
sur
, toute
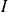-solution est de classe
sur
.
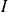Définition :
Une solution
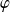de
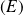définie sur
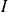est une solution maximale si elle ne peut pas être prolongée en une solution sur un intervalle
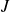contenant strictement
.
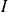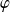est une solution maximale s'il n'existe pas un intervalle
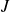contenant strictement
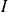et une
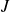- solution
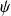de
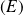telle que :
.
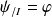En particulier, toute solution sur
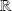est évidemment maximale.
Si
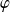est une solution maximale de
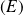définie sur
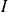et si
, la restriction de
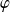à
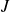est une
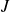-solution de
.
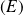Fondamental :
Théorème de Cauchy-Lipschitz
Soit
un espace vectoriel normé de dimension finie,
un ouvert de
et
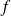une application de classe
sur
à valeurs dans
.
Les solutions maximales de l'équation différentielle
sont définies sur des intervalles ouverts.Pour tout
, il existe une unique solution maximale
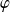définie sur un intervalle
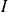contenant
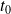qui vérifie :
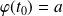.L'ensemble des graphes des solutions maximales forment une partition de
.Toute solution de l'équation différentielle est la restriction d'une et une seule solution maximale.
La détermination des solutions maximales permet donc d'avoir toutes les solutions.
Définition :
Une équation différentielle autonome d'ordre
est une équation de la forme :
où
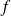est une fonction continue.
Propriétés :
Si
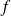est de classe
à valeurs dans
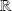, les solutions maximales sont constantes ou injectives.Si
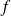est de classe
à valeurs dans
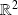, les solutions maximales sont injectives ou périodiques définies sur
.
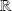