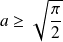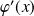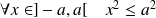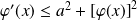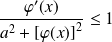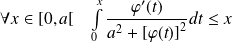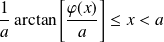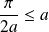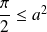Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
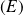l'équation différentielle :
.
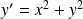Question
Justifier l'existence d'une unique solution maximale
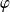qui vérifie :
.
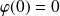Utilisez le théorème de Cauchy-Lipschitz.
Soit
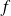la fonction polynômiale définie par :
.
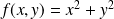La fonction
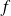est de classe
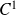sur l'ouvert
.
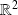On peut donc appliquer le théorème de Cauchy-Lipschitz.
Conclusion : Il existe une unique solution maximale
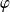qui vérifie :
.
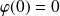Question
Démontrer que
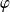est une fonction impaire.
Introduisez la fonction
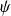définie par :
.
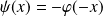La fonction
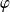est définie sur un intervalle ouvert
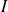contenant
.
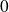Soit
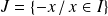et
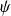la fonction définie par :
.
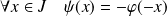Donc :
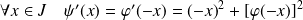car
.
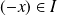Donc :
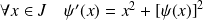et :
.
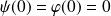Donc
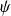est une solution de
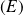qui vérifie :
.
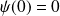Donc
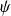est une restriction de la solution maximale
:
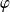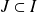et :
.
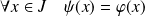Donc l'intervalle
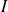est symétrique par rapport à
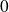et :
.
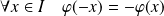Conclusion : La fonction
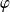est impaire.
Question
Démontrer que l'ensemble de définition de
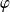est un intervalle de la forme
.
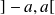Raisonnez par l'absurde.
On sait que
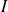est un intervalle ouvert symétrique par rapport à
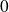. Donc
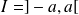s'il est borné, et
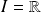sinon.
On raisonne par l'absurde en supposant que :
.
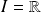Alors :
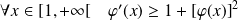, donc :
.
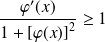Donc, en intégrant :
.
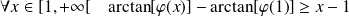On aboutit à une absurdité car la fonction Arctangente est majorée par
.
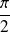Conclusion :
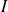est un intervalle borné de la forme
.
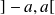Question
Déterminer les limites de
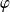en
et en
.
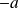Montrez que la fonction
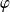ne peut pas admettre une limite finie en raisonnant par l'absurde.
La fonction
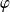est continue et croissante sur
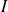car :
.
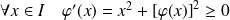Donc la fonction
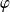admet une limite en
.
Si
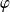admet une limite finie
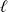en
, on peut prolonger
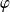par continuité en
.
Son prolongement est défini par :
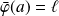et :
.
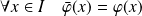Donc :
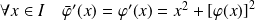. Donc :
.
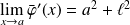Donc
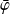est dérivable en
et :
.
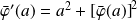Donc
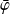est une solution de
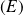sur
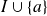, ce qui est absurde car
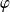est maximale.
Donc
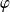n'admet pas de limite finie en
(ni en
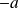car
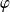est impaire).
Conclusion :
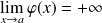et
.
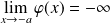Question
Question
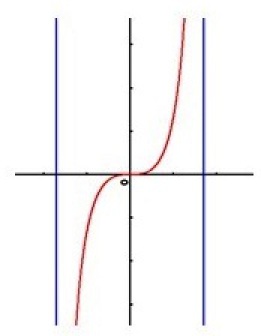
Donner le tableau de variations de
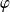et l'allure de sa courbe représentative.
La fonction
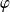est croissante sur
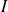et
.
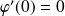