Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
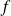 la fonction définie par :
la fonction définie par :
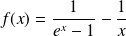 .
.
Question
Démontrer que la fonction
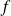 admet un prolongement de classe
admet un prolongement de classe
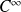 sur
sur
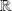 .
.
Montrer que la fonction peut s'écrire comme quotient de deux fonctions développables en série entière, le dénominateur ne s'annulant pas.
La fonction
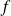 est définie et de classe
est définie et de classe
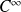 sur
sur
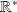 car les dénominateurs ne s'annulent pas.
car les dénominateurs ne s'annulent pas.
Il s'agit donc d'étudier le prolongement en
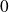 .
.
On peut remarquer que :
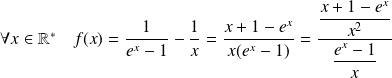 .
.
Or :
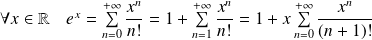 .
.
Et :
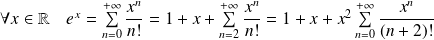 .
.
Donc :
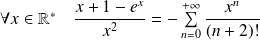 et :
et :
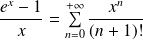 .
.
Soit
 la fonction définie par :
la fonction définie par :
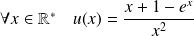 et :
et :
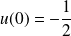 .
.
Soit
 la fonction définie par :
la fonction définie par :
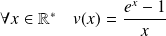 et :
et :
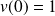 .
.
Alors :
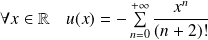 et :
et :
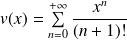 .
.
Les deux fonctions sont développables en série entière, donc de classe sur
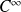 sur
sur
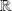 .
.
Or :
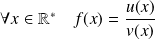 . Donc on peut prolonger la fonction
. Donc on peut prolonger la fonction
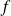 en
en
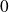 en posant :
en posant :
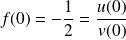 .
.
Le prolongement de la fonction
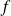 est donc quotient de deux fonctions de classe
est donc quotient de deux fonctions de classe
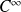 sur
sur
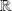 .
.
On peut remarquer que le dénominateur ne s'annule pas en étudiant la fonction
 .
.
En effet :
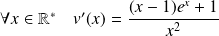 est du signe de :
est du signe de :
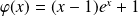 .
.
Or :
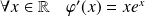 . Donc
. Donc
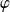 admet un minimum en
admet un minimum en
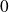 et :
et :
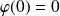 .
.
Donc la fonction
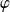 est positive ou nulle sur
est positive ou nulle sur
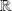 .
.
Donc la fonction
 est croissante sur
est croissante sur
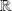 . Or :
. Or :
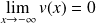 . Donc :
. Donc :
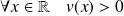 .
.
Conclusion : La fonction
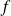 admet un prolongement de classe
admet un prolongement de classe
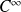 sur
sur
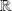 .
.





