Développement d'une fonction en série entière
Fondamental :
Propriétés des sommes de séries entières d'une variable réelle
Soit
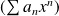 une série entière de rayon de convergence
une série entière de rayon de convergence
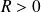 et soit
et soit
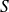 sa somme :
sa somme :
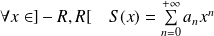 .
.
Continuité : La somme
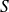 est continue sur
est continue sur
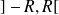 .
.
Primitive : Le rayon de convergence de la série entière
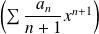 est
est
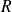 et :
et :
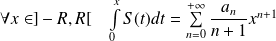 .
.
Dérivation : Le rayon de convergence de la série entière
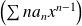 est
est
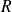 .
. La somme
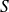 est dérivable et :
est dérivable et :
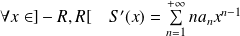 .
. La somme
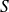 est même
est même
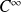 sur
sur
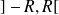 et :
et :
 .
.
On se pose le problème inverse : toute fonction est-elle somme d'une série entière ?
Définition :
Une fonction
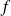 définie sur
définie sur
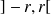 (
(
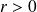 ) est développable en série entière s'il existe une série entière
) est développable en série entière s'il existe une série entière
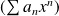 de rayon de convergence
de rayon de convergence
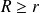 telle que :
telle que :
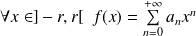 .
.
Alors la fonction
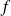 est
est
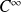 et :
et :
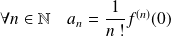 .
.
Si
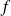 est développable en série entière, il y a donc unicité de cette série et :
est développable en série entière, il y a donc unicité de cette série et :
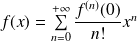 .
.
Définition :
La série de Taylor associée à une fonction
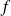 de classe
de classe
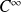 sur
sur
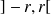 (
(
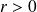 ) est la série entière
) est la série entière
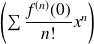 .
.
Mais, la série de Taylor de
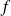 peut converger sans que
peut converger sans que
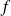 en soit la somme.
en soit la somme.
Par exemple, la fonction
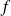 définie par :
définie par :
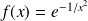 si
si
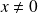 et
et
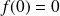 est de classe
est de classe
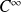 sur
sur
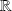 , et toutes ses dérivées sont nulles en
, et toutes ses dérivées sont nulles en
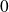 . Donc sa série de Taylor converge et elle est nulle, et donc sa somme n'est pas égale à
. Donc sa série de Taylor converge et elle est nulle, et donc sa somme n'est pas égale à
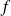 .
.
Toutes les fonctions ne sont donc pas développables en série entière.
Fondamental :
Une fonction
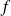 définie sur
définie sur
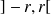 (
(
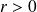 ) est développable en série entière si et seulement si :
) est développable en série entière si et seulement si :
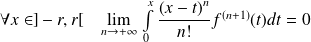 .
.
C'est une conséquence de la formule de Taylor avec reste intégral :
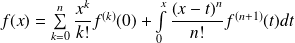 .
.
En particulier, s'il existe une constante
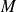 telle que
telle que
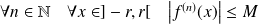 , alors la fonction
, alors la fonction
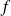 est développable en série entière.
est développable en série entière.
Fondamental :
Les fonctions suivantes sont développables en séries entières :
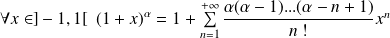 .
.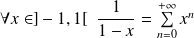 .
.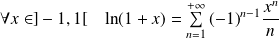 .
.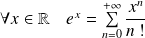 .
.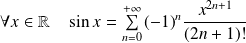 .
.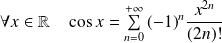 .
.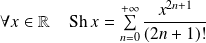 .
.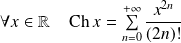 .
.





