Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
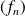la suite de fonctions définies par :
.
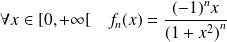Question
Etudier la convergence de la série
.
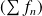Utilisez le critère spécial des séries alternées.
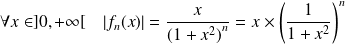, et :
.
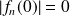On reconnaît une série géométrique. Or :
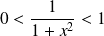si
.
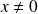Donc la série
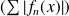est convergente pour tout
.
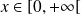Donc la série
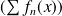est absolument convergente, donc convergente pour tout
.
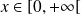Conclusion : La série
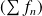converge simplement sur
.
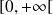Les fonctions
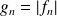sont dérivables sur
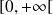et :
.
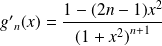On obtient le tableau de variations suivant :
Donc :
.
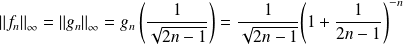Or :
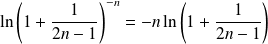, donc :
.
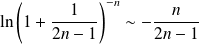Donc :
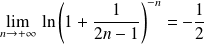. Donc :
.
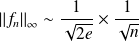Or la série de Riemann
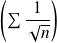est divergente. Donc la série
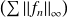est divergente.
Conclusion : La série
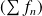ne converge pas normalement sur
.
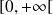Or la série
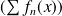est une série alternée dont le terme général tend vers
.
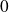On peut remarquer que, pour tout entier
:
.
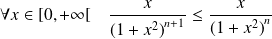Donc il s'agit d'une série alternée dont le terme général décroit vers
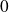en valeur absolue.
Donc la série
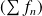est uniformément convergente si et seulement si la suite
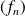converge uniformément vers la fonction nulle.
Or :
.
Conclusion : La série
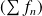converge uniformément sur
.
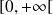