Convergence d'une série de fonctions
Les fonctions sont définies sur un intervalle
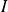de
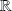à valeurs réelles ou complexes.
Une série de fonctions
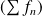est la suite des sommes partielles
.
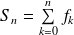Définition :
Convergence simple (ou ponctuelle)
Une série de fonctions
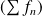converge simplement sur
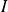si la suite des sommes partielles
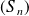converge simplement sur
.
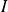La limite
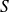de la suite
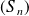est la somme de la série, notée
.
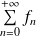Donc la série de fonctions
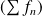converge simplement sur
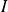si et seulement si la série numérique
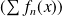converge pour tout
.
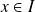Alors :
.
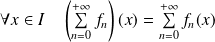Et l'on peut définir la suite
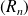des restes :
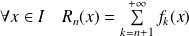. Elle converge simplement vers la fonction nulle.
Définition :
Convergence uniforme
Une série de fonctions
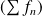converge uniformément sur
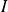si la suite des sommes partielles
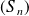converge uniformément sur
.
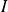Fondamental :
Propriétés
Une série de fonctions
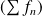converge uniformément si et seulement si la série converge simplement et si la suite
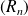des restes converge uniformément vers la fonction nulle. Si la série de fonctions
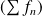converge uniformément, alors la suite
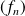converge uniformément vers la fonction nulle.
Donc s'il existe une suite
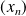de
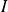telle que
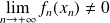, la série
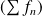ne converge pas uniformément sur
.
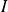Fondamental :
Cas des séries alternées
Soit une série de fonctions
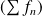telle que, pour tout
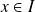, la série numérique
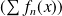soit une série alternée dont le terme général décroît en valeur absolue vers
.
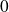Alors la série
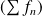converge uniformément sur
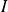si et seulement si la suite
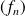converge uniformément sur
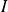vers la fonction nulle.
Le troisième mode de convergence va donner une condition suffisante de convergence uniforme.
Définition :
Convergence normale
Une série
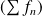de fonctions bornées sur
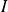converge normalement sur
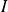si la série
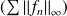converge.
On rappelle que :
.
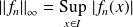Donc s'il existe une série positive convergente
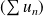telle que :
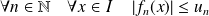, alors la série
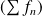converge normalement.
Si la série
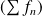converge normalement :
.
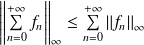Fondamental :
La convergence normale entraîne la convergence uniforme.
Donc pour démontrer qu'une série de fonctions converge uniformément, on peut :
soit montrer qu'elle converge simplement et qu'il existe une suite numérique
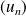convergeant vers
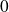telle que :
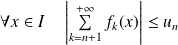.soit montrer qu'elle converge normalement en montrant il existe une série positive convergente
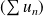telle que :
.
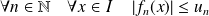