Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Soit
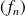et
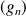les suites de fonctions définies par :
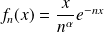et
.
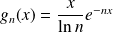Question
Etudier la convergence de la série
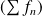suivant les valeurs du réel
.
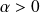Utilisez les croissances comparées.
Pour les convergences uniforme et normale, calculez le maximum de
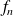sur
.
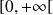Si
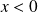, alors :
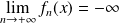. Donc la série
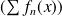diverge.
Si
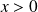, alors :
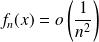. Donc la série
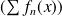converge.
Et si
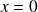, la série est nulle, donc convergente.
Conclusion : Pour tout
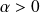, la série
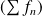converge simplement sur
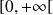et diverge sur
.
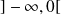Les fonctions
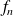sont positives et dérivables sur
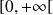. Et :
.
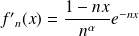On obtient le tableau de variations suivant :
Donc le maximum de
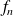sur
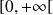est :
.
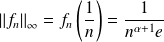Or :
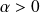, donc :
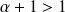. Donc la série
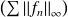est convergente.
Conclusion : Pour tout
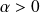, la série
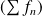converge normalement, donc uniformément sur
.
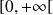Question
Etudier la convergence de la série
.
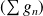Utilisez les croissances comparées.
Pour les convergences uniforme et normale, calculez le maximum de
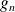sur
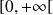, et majorez le reste de la série.
L'étude de la convergence simple est identique à celle de la série
.
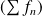Si
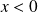, alors :
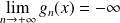. Donc la série
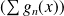diverge.
Si
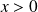, alors :
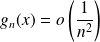. Donc la série
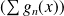converge.
Et si
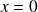, la série est nulle, donc convergente.
Conclusion : La série
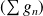converge simplement sur
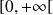et diverge sur
.
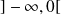Les fonctions
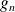sont positives et dérivables sur
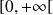. Et :
.
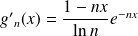On obtient le tableau de variations suivant :
Donc le maximum de
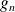sur
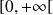est :
.
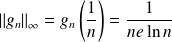La série
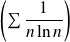est de même nature que l'intégrale
.
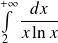Or :
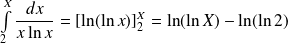. Donc :
.
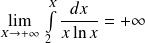Donc l'intégrale
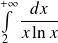et la série
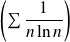sont divergentes.
Donc la série
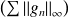est divergente.
Conclusion : La série
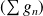ne converge pas normalement sur
.
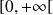Pour voir si la convergence est uniforme, on étudie le reste de la série.
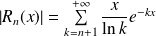. Donc :
.
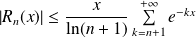Or :
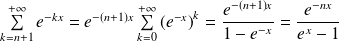si
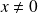. Et :
.
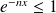Donc :
.
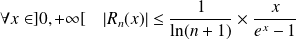Or, par convexité :
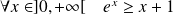, donc :
.
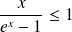Donc :
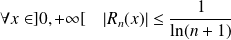et :
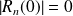. Or :
.
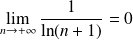Donc la suite
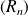converge uniformément vers la fonction nulle sur
.
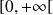Conclusion : La série
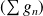converge uniformément sur
.
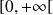