Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On munit l'espace vectoriel
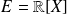de la norme :
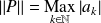si
.
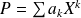On définit la suite de terme général
.
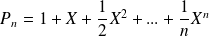Question
Montrer que la suite
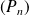est une suite de Cauchy.
Calculez
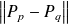en fonction des entiers
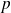et
.
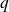Pour tous entiers
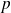et
:
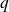Si
:
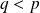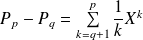. Donc :
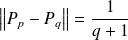.Si
:
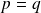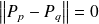.Si
:
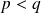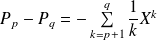. Donc :
.
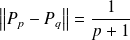Donc, pour tous les entiers
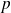et
:
.
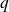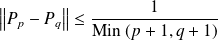Donc, si
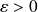, pour que
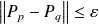, il suffit que :
.
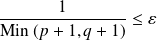Donc il suffit que
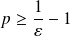et
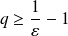. Soit
.
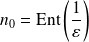Donc :
.
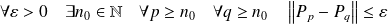Conclusion : La suite
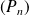est une suite de Cauchy.
Question
Montrer que la suite
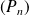est divergente.
Raisonnez par l'absurde.
On raisonne par l'absurde en supposant que la suite
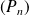converge vers un polynôme
.
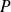Donc :
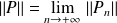. Or :
.
Donc :
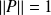. Donc
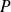n'est pas le polynôme nul.
Soit
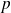le degré de
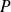. Donc :
.
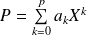Si
:
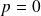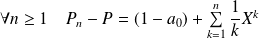, donc :
.
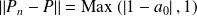Si
:
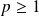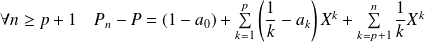.Donc :
.
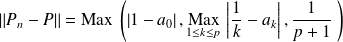Donc, dans les deux cas :
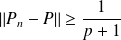. Donc :
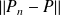ne tend pas vers
.
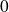Conclusion : La suite
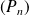est divergente.
Donc l'espace vectoriel
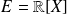n'est pas complet pour cette norme.
En fait, on peut démontrer que
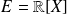n'est complet pour aucune norme.
