Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
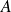une matrice carrée d'ordre
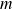à coefficients complexes.
On suppose que la suite
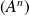converge vers une limite
.
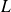Question
Démontrer que :
.
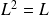Remarque :
On peut remarquer que la norme n'est pas précisée car l'espace vectoriel
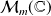est de dimension finie, et donc toutes les normes sont équivalentes.
Par hypothèse :
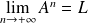, donc :
.
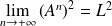Or :
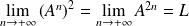, et la limite est unique.
Conclusion : La limite vérifie
.
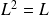Question
Montrer que la suite de terme général
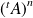est convergente. Préciser sa limite.
Pour toute matrice
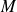, comparez la norme de
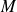et la norme de sa transposée
.
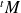Considérons par exemple la norme définie par :
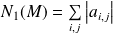si
.
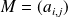On peut remarquer que :
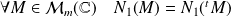car
.
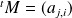Donc :
.
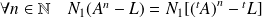Or la suite
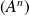converge vers
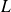. Donc :
.
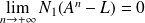Donc :
.
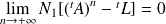Conclusion : La suite de terme général
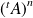converge vers
.
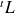Question
Si la matrice
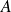est symétrique, que peut-on en déduire pour la matrice
?
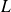Si la matrice
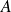est symétrique, alors :
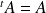, donc :
.
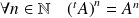Donc par unicité de la limite :
.
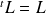Conclusion : Si la matrice
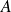est symétrique, alors la limite
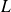est symétrique.
Question
Si la matrice
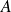est antisymétrique, que peut-on en déduire pour la matrice
?
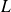Utilisez les suites des puissances paires et des puissances impaires.
Si la matrice
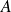est antisymétrique, alors :
.
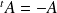Donc :
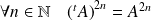et
.
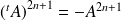Donc la suite extraite de terme général
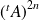converge vers
.
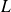Et la suite extraite de terme général
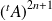converge vers
.
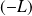Or on a vu que la suite de terme général
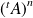converge vers
.
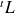Donc les deux suites extraites ont la même limite :
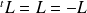. Donc :
.
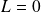Conclusion : Si la matrice
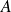est antisymétrique, alors la limite
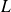est nulle.
