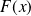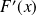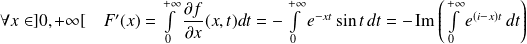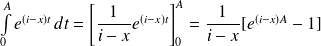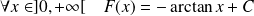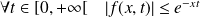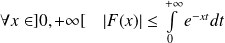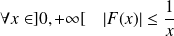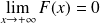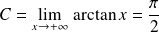Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Cet exercice propose une autre méthode de calcul de l'intégrale de Dirichlet :
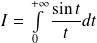déjà étudiée dans l'exercice
.
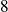On ne redémontrera donc pas ici la convergence de cette intégrale.
Soit
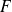la fonction définie par :
.
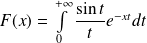Question
Démontrer que la fonction
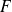est de classe
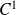sur
.
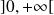Utilisez les théorèmes du cours avec une domination locale.
La fonction
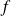définie par :
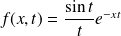est continue sur
.
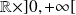On peut la prolonger par continuité pour
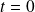en posant :
.
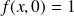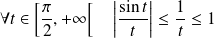, et par convexité :
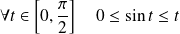. Donc :
.
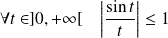Donc, pour tout
:
.
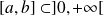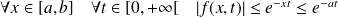Or la fonction
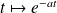est intégrable sur
.
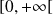Donc, par domination locale, la fonction
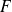est continue sur
.
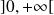La fonction
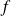admet une dérivée partielle continue sur
:
.
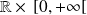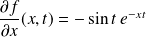Et, pour tout
:
.
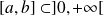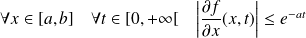Or la fonction
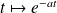est intégrable sur
.
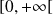Conclusion : La fonction
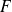est de classe
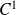sur
.
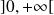Question
Question
Démontrer que la fonction
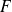est continue en
.
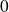Démontrez que
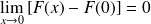en utilisant un changement de variable.
Introduisez la fonction
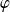définie par :
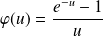si
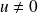et prolongée par continuité en
.
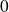La fonction
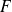est définie en
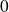puisque
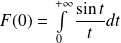, intégrale de Dirichlet.
.
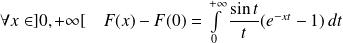On pose :
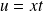, donc :
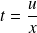et :
.
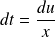Donc :
.
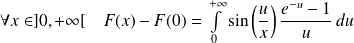Soit
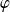la fonction définie par :
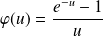si
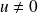et
.
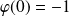La fonction
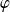est continue sur
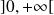et en
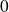car :
.
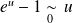La fonction
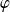est de classe
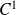sur
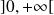et :
.
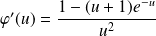Or, au voisinage de
:
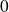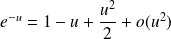, donc :
.
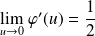Donc la fonction
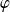est de classe
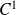sur
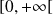et :
.
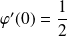Pour tout
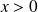, on intègre par parties :
.
.
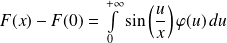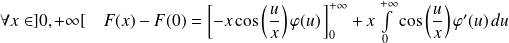Or :
.
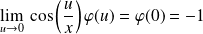Et :
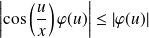, donc :
car :
.
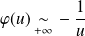Donc :
.
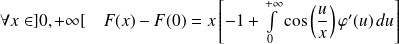Donc :
.
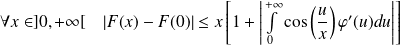Or :
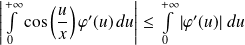et :
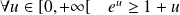, donc :
.
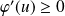Donc :
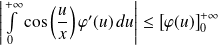. Or :
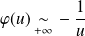, donc :
.
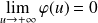Donc :
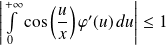. Donc :
.
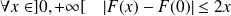Donc :
.
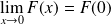Conclusion : La fonction
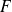est continue en
.
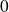Question
En déduire la valeur de l'intégrale de Dirichlet :
.
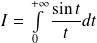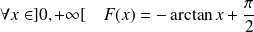, donc :
.
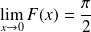Or l'intégrale de Dirichlet est égale à
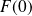et
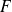est continue en
.
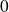Conclusion : L'intégrale de Dirichlet
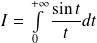est égale à
.
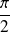