Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
et
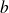deux réels tels que :
.
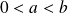Question
Démontrer que l'intégrale
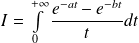est convergente, et la calculer.
Séparez l'étude en deux pour isoler les bornes impropres.
Pour chaque étude, effectuez des changements de variables pour vous ramener à des intégrales entre
et
.
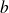La fonction
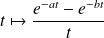est continue sur
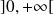et
.
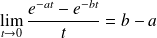Donc l'intégrale est impropre en
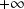et « faussement impropre » en
.
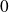Donc on étudie la convergence des intégrales
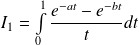et
.
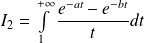Etude de
:
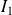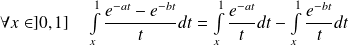.Dans la première intégrale, on pose
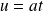et dans la deuxième
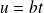.Donc :
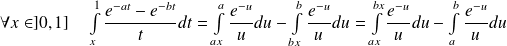.Or, en posant :
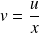, on obtient :
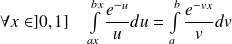.Or, par convexité :
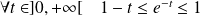. Donc :
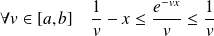.Donc :
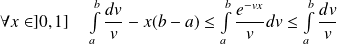. Donc :
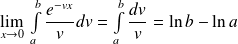.Donc l'intégrale
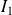est convergente et :
.
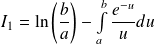Etude de
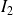:On effectue un calcul analogue avec les mêmes changements de variables.
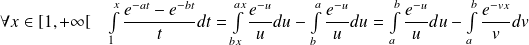.Or, par convexité :
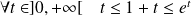, donc :
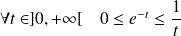.Donc :
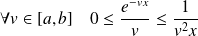. Donc :
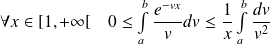.Or :
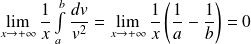. Donc :
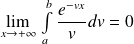. Donc :
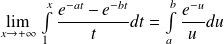.Donc l'intégrale
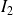est convergente et :
.
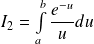Les deux intégrales sont convergentes, donc l'intégrale
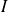est convergente et :
.
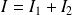Conclusion : L'intégrale
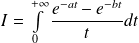est convergente, et
.
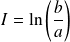Question
En déduire la convergence et le calcul de l'intégrale :
.
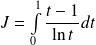Effectuez un changement de variable.
La fonction
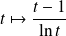est continue sur
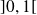avec
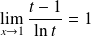et
.
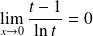Donc l'intégrale est « faussement impropre » en
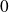et en
. Donc l'intégrale
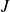est convergente.
On effectue le changement de variable :
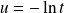, donc :
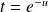et :
.
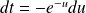Donc :
.
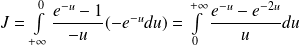On retrouve l'intégrale de la question précédente pour
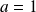et
.
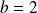Conclusion : L'intégrale
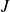est convergente et
.
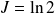