Intégration sur un intervalle quelconque
Les fonctions considérées sont définies sur un intervalle
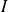de
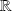et à valeurs réelles ou complexes.
Définition :
Convergence d'une intégrale sur un intervalle [a,b[
Soit
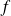une fonction continue par morceaux sur
(
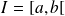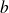réel ou
).
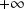L'intégrale
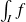est convergente si la fonction
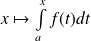a une limite finie en
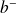(ou
).
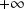Par définition :
.
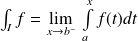Sinon, on dira que l'intégrale
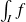est divergente.
L'intégrale « impropre » est notée
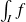ou
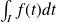ou même
.
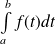Attention :
Donc, avant de manipuler toute intégrale, il faut justifier sa convergence.
Cependant, si
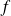est continue par morceaux sur
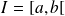et admet une limite finie en
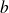, elle peut être prolongée en une fonction
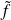continue par morceaux sur
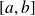. Alors l'intégrale
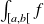est convergente et
.
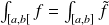On dira que l'intégrale
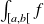est « faussement impropre ».
Fondamental :
Pour tout
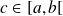, les intégrales
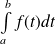et
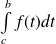sont de même nature.
Cela signifie qu'elles sont soit toutes les deux convergentes, soit toutes les deux divergentes.
Définition :
Convergence d'une intégrale sur un intervalle ]a,b]
Soit
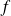une fonction continue par morceaux sur
(
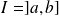réel ou
).
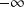L'intégrale
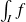est convergente si la fonction
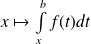a une limite finie en
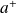(ou
).
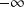Par définition :
.
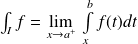Sinon, on dira que l'intégrale
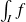est divergente.
L'intégrale est notée
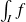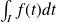ou
ou
.
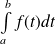Et pour tout
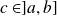, les intégrales
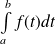et
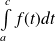sont de même nature.
Définition :
Convergence d'une intégrale sur un intervalle ]a,b[
Soit
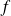une fonction continue par morceaux sur
(
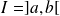et
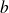réels ou infinis).
L'intégrale
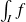est convergente s'il existe
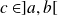tel que les deux intégrales
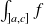et
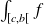soient convergentes.
Alors
.
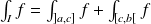Sinon, on dira que l'intégrale
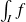est divergente.
En tenant compte des remarques faites précédemment, on peut voir que le choix de
est arbitraire.
Fondamental :
Propriétés
Sous réserve de convergence de toutes les intégrales mises en jeu, les propriétés des intégrales sur un segment s'étendent : linéarité, relation de Chasles, intégration par parties, changement de variable.
Si
converge et si
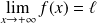, alors
.
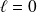Donc si
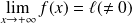, alors
diverge.
