Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
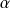un réel strictement positif.
Question
Etudier la convergence de l'intégrale
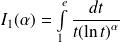suivant les valeurs de
.
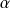Utilisez un changement de variable pour calculer l'intégrale de
à
.
L'intégrale est impropre en
, donc on étudie la limite de
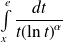en
.
On suppose d'abord
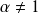et l'on pose :
.
.
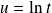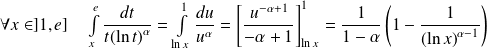Et pour
:
.
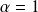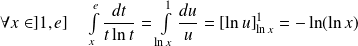Or :
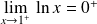, donc :
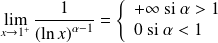et :
.
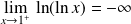Donc :
.
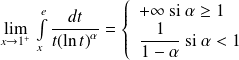Conclusion : L'intégrale
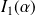est convergente si et seulement si
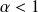et
.
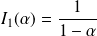Question
Etudier la convergence de l'intégrale
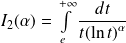suivant les valeurs de
.
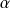Utilisez un changement de variable pour calculer l'intégrale de
à
.
L'intégrale est impropre en
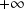, donc on étudie la limite de
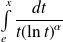en
.
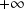On effectue un calcul analogue au précédent.
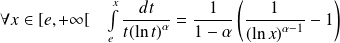si
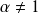, et :
.
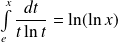Or :
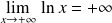, donc
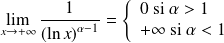et
.
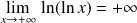Donc :
.
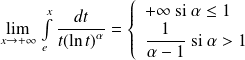Conclusion : L'intégrale
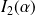est convergente si et seulement si
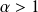et
.
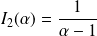Question
Pour quelles valeurs de
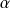l'intégrale
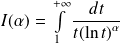est-elle convergente ?
Utilisez les questions précédentes.
L'intégrale est impropre en
et en
.
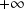Donc il faut étudier la convergence de
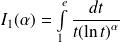et de
.
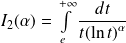Or ces deux intégrales ne sont jamais simultanément convergentes :
Si
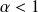, alors
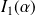est convergente et
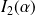est divergente.Si
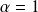, alors
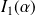et
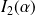sont divergentes.Si
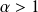, alors
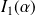est divergente et
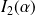est convergente.
Conclusion : L'intégrale
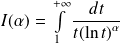est divergente pour tout réel
.
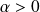