Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer que l'intégrale
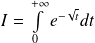est convergente et la calculer.
Indice
Utilisez un changement de variable pour calculer l'intégrale de
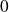à
.
Solution
La fonction
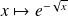est continue sur
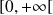. Donc l'intégrale est impropre seulement en
.
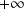On étudie donc la limite en
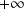de :
.
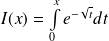Or :
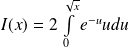en posant
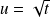, donc
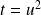et
.
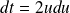On intègre par parties :
.
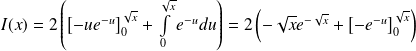Donc :
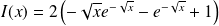. Or :
.
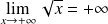Donc :
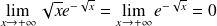. Donc :
.
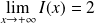Conclusion : L'intégrale
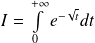est convergente et
.
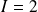