Exo 20
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient deux réels
 et
et
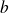 tels que :
tels que :
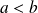 . Soient
. Soient
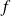 et
et
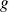 deux fonctions continues sur
deux fonctions continues sur
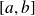 et à valeurs réelles.
et à valeurs réelles.
On suppose que
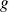 est de signe constant sur
est de signe constant sur
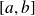 .
.
Question
Démontrer que :
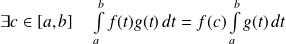 .
.
Utilisez le théorème des valeurs intermédiaires.
La fonction
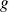 est de signe constant sur
est de signe constant sur
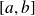 . Supposons par exemple que
. Supposons par exemple que
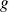 est positive.
est positive.
Si
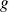 est la fonction nulle, le résultat est évident.
est la fonction nulle, le résultat est évident.
Dans la suite, on supposera que
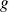 n'est pas la fonction nulle.
n'est pas la fonction nulle.
Donc :
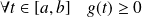 et :
et :
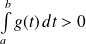 .
.
La fonction
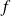 est continue sur
est continue sur
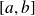 , donc l'image de
, donc l'image de
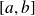 est un intervalle :
est un intervalle :
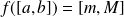 .
.
Donc :
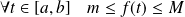 , donc :
, donc :
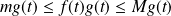 .
.
Or
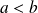 . Donc :
. Donc :
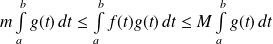 .
.
Donc le quotient
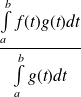 appartient à
appartient à
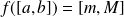 .
.
Conclusion :
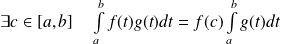 .
.
Soient deux réels
 et
et
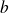 tels que :
tels que :
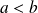 . Soit
. Soit
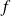 une fonction de classe
une fonction de classe
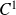 sur
sur
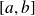 et à valeurs réelles.
et à valeurs réelles.
On pose :
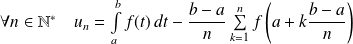 .
.
Question
Déterminer la limite de la suite
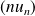 .
.
Exprimez
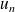 comme une somme d'intégrales et introduisez le taux d'accroissement de
comme une somme d'intégrales et introduisez le taux d'accroissement de
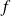 sur chaque intervalle.
sur chaque intervalle.
On reconnaît une somme de Riemann, donc on sait déjà que
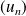 converge vers
converge vers
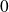 .
.
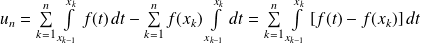 si l'on pose :
si l'on pose :
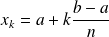 .
.
Soit
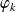 la fonction définie sur
la fonction définie sur
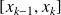 par :
par :
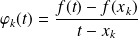 si
si
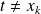 et
et
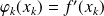 .
.
Donc :
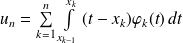 .
.
La fonction
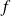 est dérivable, donc la fonction
est dérivable, donc la fonction
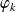 est continue sur
est continue sur
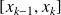 . Et la fonction
. Et la fonction
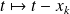 est de signe constant.
est de signe constant.
Donc, d'après la question précédente :
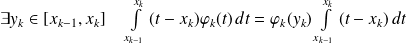 .
.
La fonction
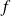 est de classe
est de classe
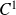 sur
sur
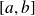 , donc sur
, donc sur
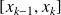 .
.
Donc d'après le théorème des accroissements finis :
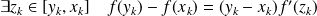 .
.
Donc :
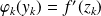 et
et
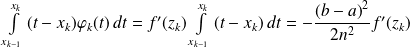 .
.
Donc :
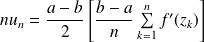 avec :
avec :
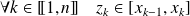 .
.
On reconnaît une somme de Riemann de la fonction
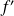 qui est continue sur
qui est continue sur
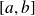 . Donc :
. Donc :
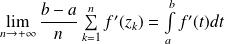 .
.
Conclusion :
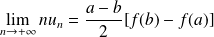 .
.





