Exo 19
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
 une fonction continue de
une fonction continue de
 dans
dans
 .
.
On définit la suite de terme général :
 .
.
Question
On suppose d'abord que la fonction
 est de classe
est de classe
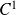 sur l'intervalle
sur l'intervalle
 .
.
Montrer que la suite
 est convergente et calculer sa limite.
est convergente et calculer sa limite.
Intégrez par parties.
 . Donc :
. Donc :
 .
.
On suppose que
 est de classe
est de classe
 sur
sur
 , donc on peut intégrer par parties.
, donc on peut intégrer par parties.
 .
.
Or
 est continue sur
est continue sur
 , donc bornée :
, donc bornée :
 .
.
Donc :
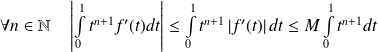 .
.
Donc :
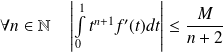 .
.
Donc :
 .
.
Conclusion : La suite
 est convergente et
est convergente et
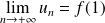 .
.
Question
Démontrer que le résultat précédent reste vrai dans le cas général.
Séparez l'intervalle
 en deux intervalles pour majorer
en deux intervalles pour majorer
 .
.
On ne suppose plus que
 est de classe
est de classe
 sur
sur
 , et il s'agit de montrer que l'on a aussi
, et il s'agit de montrer que l'on a aussi
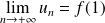 .
.
 , donc :
, donc :
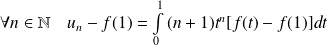 .
.
Donc :
 .
.
Soit :
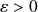 .
.
La fonction
 est continue en
est continue en
 , donc :
, donc :
 .
.
Donc :
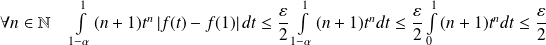 .
.
La fonction
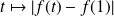 est continue sur
est continue sur
 , donc bornée, donc il existe
, donc bornée, donc il existe
 tel que :
tel que :
 .
.
Donc :
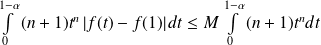 .
.
Donc :
 . Or :
. Or :
 , donc :
, donc :
 .
.
Donc :
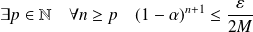 , donc :
, donc :
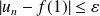 .
.
Donc :
 .
.
Conclusion : La suite
 est convergente et
est convergente et
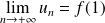 .
.





