Exo 18
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
une fonction continue de
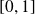dans
telle que :
.
Question
Montrer qu'il existe un réel
tel que :
.
Intégrez par parties en introduisant une primitive
de
.
Séparez l'étude en trois cas selon le signe de
.
Si
, le résultat est évident.
On suppose donc dans la suite que
n'est pas la fonction nulle.
On définit les fonctions
:
et
:
sur l'intervalle
.
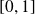Il s'agit de montrer que
s'annule au moins une fois sur
.
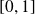Les fonctions
et
sont de classe
sur
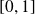, donc on peut intégrer par parties.
.
Donc :
. Donc :
et :
.
La fonction
est continue sur
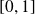, donc elle est bornée et atteint ses bornes.
Donc il existe
et
dans
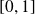tels que :
.
Or
n'est pas la fonction nulle, donc
n'est pas constante, donc :
, donc :
.
Et :
et :
.
Les fonctions
et
sont continues et de signes constants.
Donc
si et seulement si
ou si
est constante sur
.
De même
si et seulement si
ou si
est constante sur
.
Si
n'est pas de signe constant sur
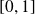, alors
et
.Or :
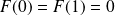. Donc
et
, et
n'est constante ni sur
, ni sur
. Donc
et
. Or
est continue, donc il existe
compris strictement entre
et
tel que
, donc
.
Si
, alors
et
.Donc
et
n'est pas constante sur
. Donc :
.De plus :
, donc
car
n'est pas la fonction nulle.Or
est continue, donc il existe
compris strictement entre
et
tel que
, donc
.
Si
, alors
et
.Donc
et
n'est pas constante sur
. Donc :
.De plus :
, donc
car
n'est pas la fonction nulle.Or
est continue, donc il existe
compris strictement entre
et
tel que
, donc
.
Donc dans tous les cas, il existe
tel que :
.
Conclusion : Il existe un réel
tel que
.
