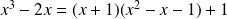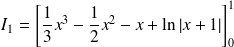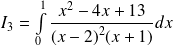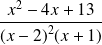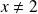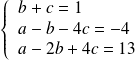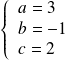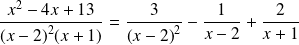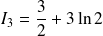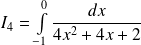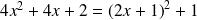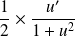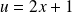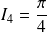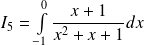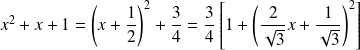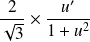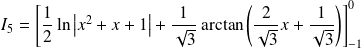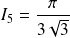Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Question
Calculer l'intégrale :
.
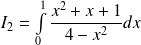Indice
Effectuez la division euclidienne du numérateur par le dénominateur, puis décomposez la fraction en éléments simples.
Solution
La division euclidienne donne :
.
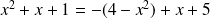Donc :
.
La fonction
a pour primitive :
.
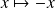La fonction
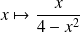est de la forme
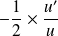avec
.
Donc une primitive de
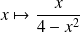est
.
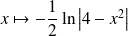On décompose
en éléments simples :
.
Donc :
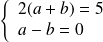. Donc :
.
Donc :
.
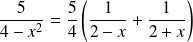Donc une primitive de
est :
.
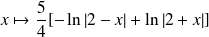Donc :
.
Conclusion :
.
