Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Dans certains cas, il peut être plus judicieux d'utiliser une subdivision qui n'est pas régulière.
Question
Construire une subdivision
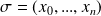de l'intervalle
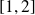telle que les
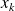forment une suite géométrique.
Si
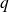est la raison de la suite, on doit avoir :
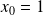et :
.
La suite doit être strictement croissante, donc :
.
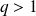Et :
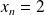, donc :
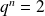, donc :
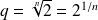(qui est bien supérieur à
).
Conclusion :
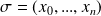avec
.
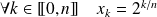Question
En déduire le calcul de l'intégrale :
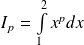pour tout entier naturel
.
Démontrez que le pas de la subdivision tend vers
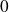et utilisez des sommes de Riemann.
.
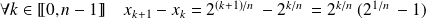Le pas de la subdivision
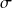est :
.
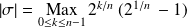Donc :
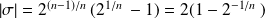. Or :
.
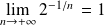Donc le pas de la subdivision tend vers
.
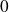Donc les sommes de Riemann correspondantes convergent vers l'intégrale
.
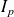Donc :
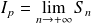où :
.
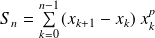Or :
.
Or :
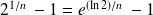, donc :
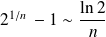car :
.
De même :
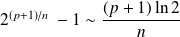. Donc :
.
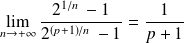Conclusion :
.
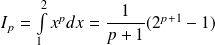