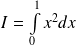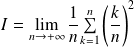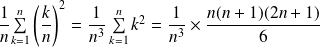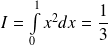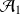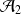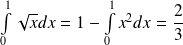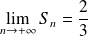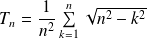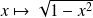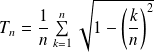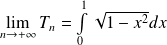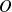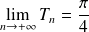Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les sommes de Riemann peuvent permettre de calculer une intégrale ou une aire.
Et inversement, si l'on connaît l'intégrale ou l'aire, on peut en déduire des limites de suites.
Question
Question
En déduire la limite de la suite de terme général :
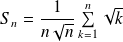 .
.
Indice
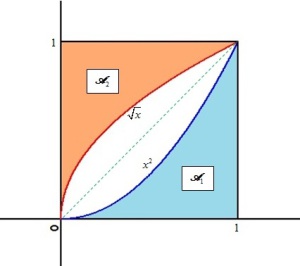
Pour calculer l'intégrale, utilisez la symétrie des courbes représentatives des fonctions
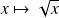 et
et
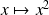 .
.
Solution
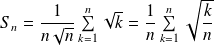 est une somme de Riemann de la fonction
est une somme de Riemann de la fonction
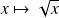 sur
sur
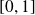 .
.
Or la fonction
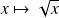 est continue sur
est continue sur
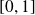 , donc :
, donc :
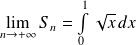 .
.
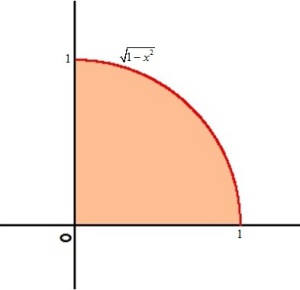
Il s'agit de l'aire située sous la courbe représentative de la fonction
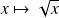 .
.