Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Démontrer qu'une fonction croissante sur un segment
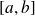(avec
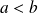) est intégrable sur
.
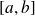Avec une subdivision régulière, construisez deux fonctions en escalier minorant et majorant la fonction.
Soit
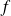une fonction croissante sur
.
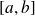Pour tout entier non nul
, on note :
.
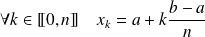La fonction est croissante. Donc :
.
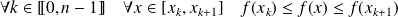Soit
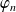la fonction définie par :
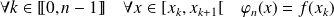et
.
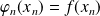La fonction
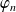est une fonction en escalier qui minore
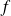. Et :
.
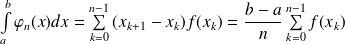Soit
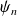la fonction définie par :
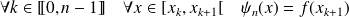et
.
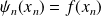La fonction
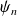est une fonction en escalier qui majore
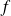. Et :
.
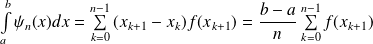Donc :
.
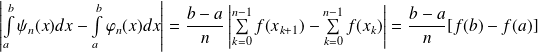Donc :
.
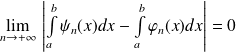Donc, pour tout
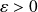, il existe deux fonctions en escalier
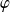et
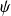telles que
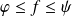et telles que :
.
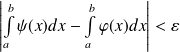Conclusion : Toute fonction croissante sur
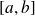est intégrable sur
.
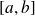