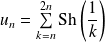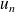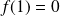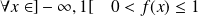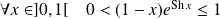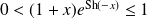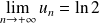Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Etudier et représenter graphiquement la fonction définie par :
.
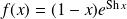Pour l'étude des variations de
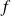, introduisez une fonction auxiliaire.
La fonction
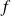est définie sur
.
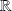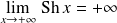, donc :
.
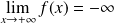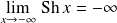, donc, au voisinage de
:
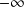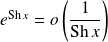, donc :
.
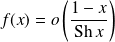Or, au voisinage de
:
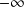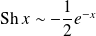, donc :
.
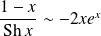Donc :
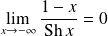, et donc :
.
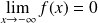La fonction
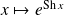est dérivable sur
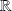comme composée de fonctions dérivables.
Donc la fonction
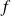est dérivable sur
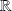comme produit de fonctions dérivables.
.
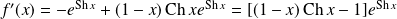Donc
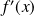est du signe de la fonction
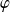définie par :
.
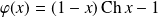Elle est dérivable sur
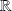, et :
.
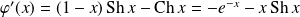Or
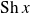est du signe de
. Donc :
, donc :
.
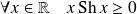Donc 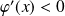la fonction
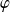est strictement décroissante sur
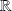. Or :
.
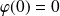Donc :
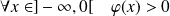et :
.
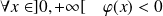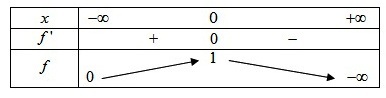
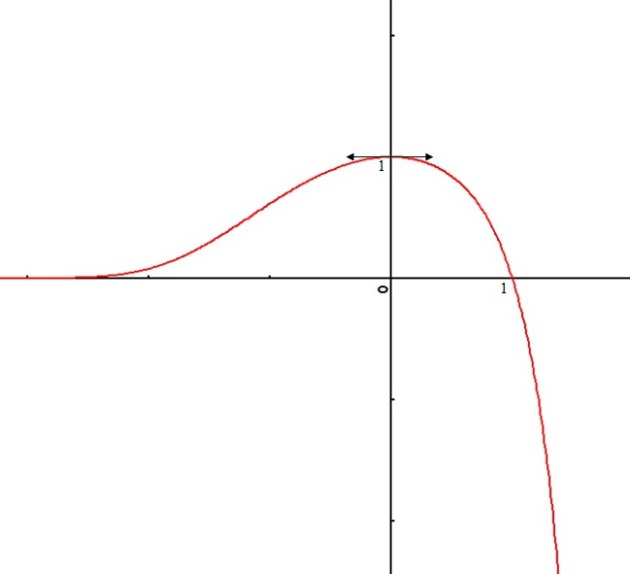
On en déduit le tableau de variations de
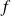et sa courbe représentative.
