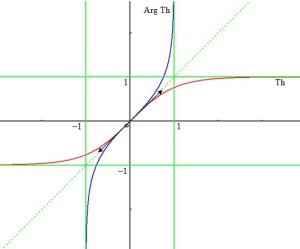
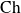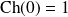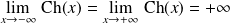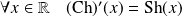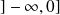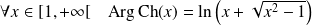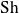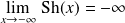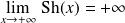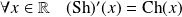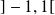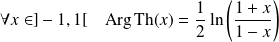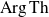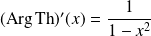Fonctions Hyperboliques et réciproques
Toute fonction définie sur
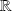se décompose de manière unique en somme d'une fonction paire et d'une fonction impaire.
Définition :
La fonction cosinus hyperbolique est la fonction définie par :
.
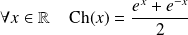La fonction sinus hyperbolique est la fonction définie par :
.
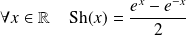Le cosinus hyperbolique est la partie paire de la fonction exponentielle, et le sinus hyperbolique est sa partie impaire.
Ces définitions sont à rapprocher des formules d'Euler.
Fondamental :
Propriétés
.
.
.
.
.
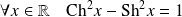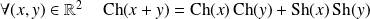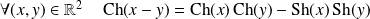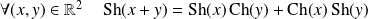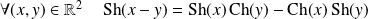Ces formules sont à rapprocher des formules de trigonométrie usuelles.
Fondamental :
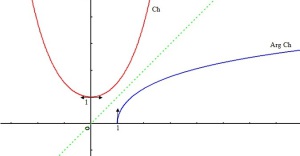
Fonction cosinus hyperbolique
|  |
Fondamental :
Fonction sinus hyperbolique
|  |
Définition :
La fonction tangente hyperbolique est définie par :
|  |
On peut également définir une cotangente hyperbolique et sa réciproque.
