Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Etudier et représenter graphiquement la fonction définie par :
.
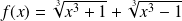Remarquez la parité de la fonction.
Pour l'étude en
, utilisez le théorème de prolongement de la dérivée.
La fonction
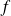est définie sur
puisque
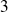est impair.
.
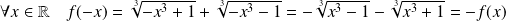Donc la fonction
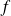est impaire, et donc on réduit l'étude à
.
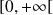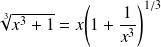, donc :
.
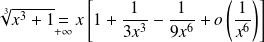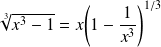, donc :
.
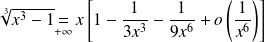Donc :
. Donc
.
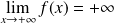La courbe de
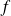admet en
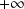une asymptote oblique d'équation
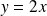et se trouve en dessous de son asymptote au voisinage de
.
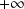Les fonctions
,
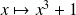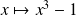et
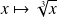sont croissantes.
Donc la fonction
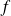est croissante comme somme de deux fonctions croissantes.
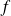est dérivable sur
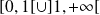et :
.
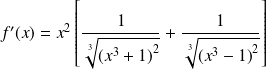Donc :
, et donc la courbe de
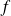a une tangente horizontale en
.
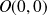Et :
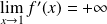. Donc, d'après le théorème de prolongement de la dérivée, la fonction
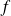n'est pas dérivable en
et la courbe a une tangente verticale en
.
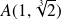On complète la courbe de
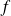par symétrie par rapport au point
.
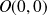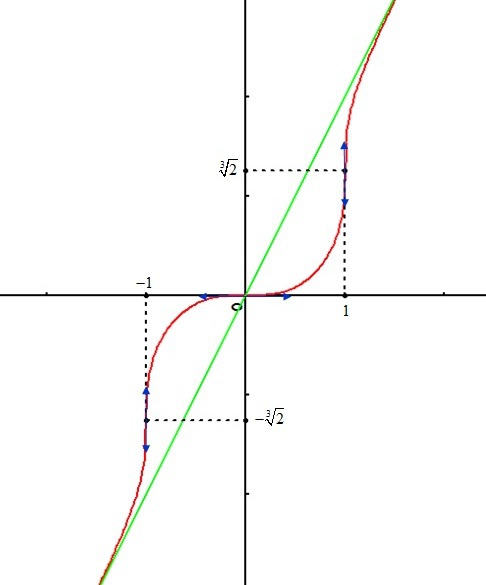
Question
Etudier et représenter graphiquement la fonction définie par :
.
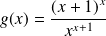Faites une étude de la fonction
.
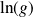La fonction
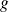est définie sur
et :
.
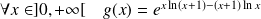Soit
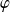la fonction définie par :
.
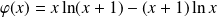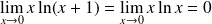, donc :
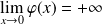, donc :
.
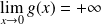La courbe de
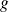admet une asymptote verticale d'équation :
.
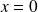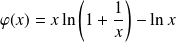et :
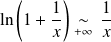. Donc :
.
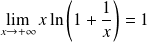Donc :
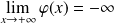, donc :
.
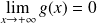La courbe de
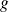admet en
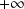une asymptote horizontale d'équation :
.
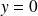La fonction
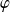est dérivable sur
, donc
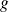est dérivable sur
.
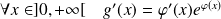, donc
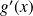est du signe de
.
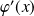Or :
.
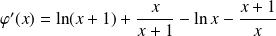On dérive une deuxième fois :
.
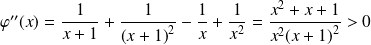Donc
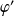est croissante sur
et :
.
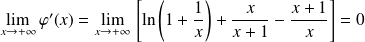Donc :
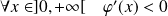, donc :
.
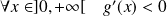