Fonctions puissances
Rappel :
Pour tout entier naturel
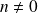 :
:
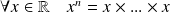 (
(
 fois).
fois).
Pour tout entier naturel
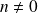 :
:
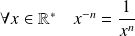 .
.
Et :
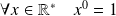 .
.
Donc :
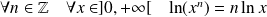 , donc :
, donc :
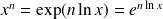 .
.
Fondamental :
Pour tout entier naturel
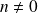 , la fonction
, la fonction
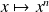 est bijective :
est bijective :
de
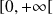 dans
dans
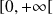 si
si
 est pair.
est pair.de
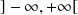 dans
dans
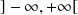 si
si
 est impair.
est impair.
Sa réciproque est notée :
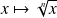 .
.
La fonction
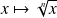 est donc définie sur
est donc définie sur
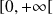 si
si
 est pair, et sur
est pair, et sur
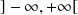 si
si
 est impair.
est impair.
Et lorsque
 est impair, la fonction
est impair, la fonction
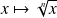 est impaire.
est impaire.
Et :
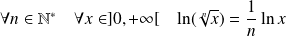 , donc :
, donc :
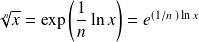 .
.
Pour tous les entiers
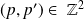 et
et
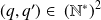 tels que
tels que
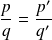 , on a :
, on a :
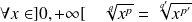 et
et
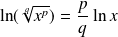 .
.
Définition :
Pour tout rationnel
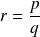 avec
avec
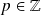 et
et
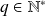 , on définit :
, on définit :
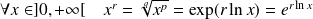 .
.
Par continuité de la fonction exponentielle, si un réel
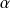 est limite d'une suite de rationnels
est limite d'une suite de rationnels
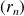 :
:
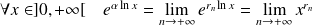 .
.
Définition :
Pour tout réel
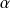 , on appelle fonction puissance
, on appelle fonction puissance
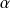 la fonction définie par :
la fonction définie par :
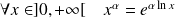 .
.
Suivant les valeurs de
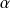 , cette fonction peut être prolongée en
, cette fonction peut être prolongée en
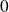 ou sur
ou sur
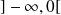 .
.
Fondamental :
Propriétés algébriques
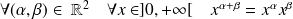 .
. .
.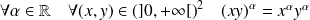 .
.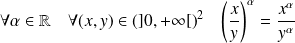 .
.
Les fonctions puissances sont solutions de l'équation fonctionnelle :
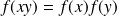 .
.
Fondamental :
Propriétés
La fonction
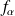 :
:
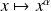 est définie, continue et indéfiniment dérivable sur
est définie, continue et indéfiniment dérivable sur
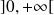 .
.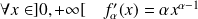 .
.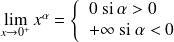 et
et
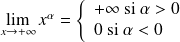 .
.Si
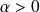 :
: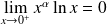 .
.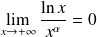 .
.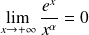 .
.
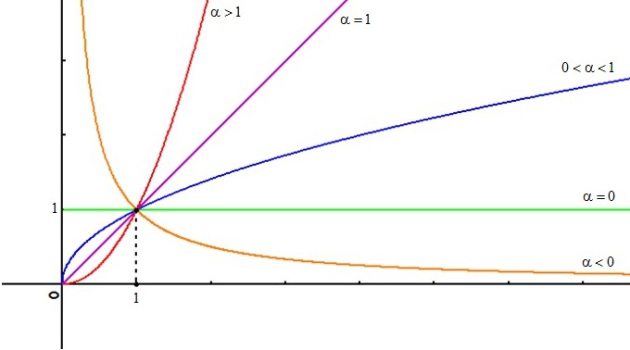
Si
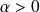 , la fonction est prolongeable par continuité en
, la fonction est prolongeable par continuité en
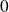 .
.
Si
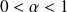 , la courbe a une tangente verticale en 0 et possède une branche parabolique de direction
, la courbe a une tangente verticale en 0 et possède une branche parabolique de direction
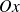 en
en
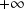 .
.
Si
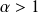 , la courbe a une tangente horizontale en 0 et possède une branche parabolique de direction
, la courbe a une tangente horizontale en 0 et possède une branche parabolique de direction
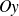 en
en
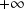 .
.





