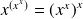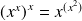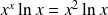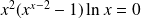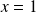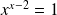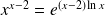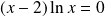Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Démontrer que :
.
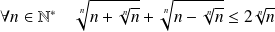Vous pouvez vous ramener soit à l'étude du sens de variations d'une fonction, soit à une étude de convexité.
Première solution
L'inégalité est équivalente à :
.
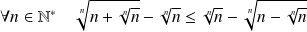Soit
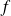la fonction définie par :
.
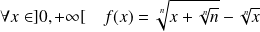L'inégalité est équivalente à :
.
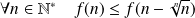La fonction
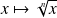est dérivable sur
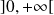, donc
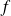est dérivable sur
.
.
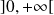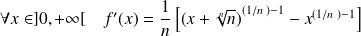Or :
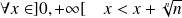et
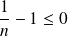. Donc :
.
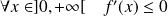Donc la fonction
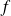est décroissante sur
.
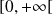Or :
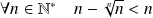, donc :
.
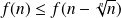Conclusion :
.
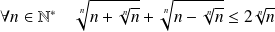Deuxième solution
La fonction
définie par :
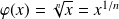est dérivable deux fois sur
.
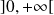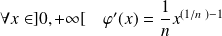et :
.
Donc :
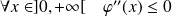. Donc la fonction
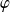est concave sur
.
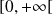Donc :
.
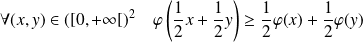Donc :
.
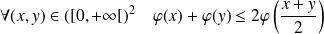Donc :
.
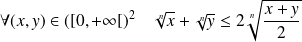On applique cette propriété à
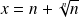et
.
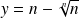Conclusion :
.
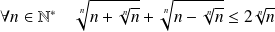