Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Etudier et représenter graphiquement la fonction définie par :
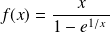 .
.
Pour étudier le sens de variations de
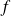 , introduisez une fonction auxiliaire.
, introduisez une fonction auxiliaire.
La fonction
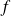 est définie si et seulement si :
est définie si et seulement si :
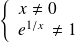 . Donc :
. Donc :
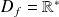 .
.
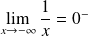 , donc :
, donc :
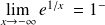 , donc :
, donc :
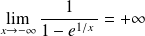 .
.
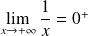 , donc :
, donc :
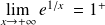 , donc :
, donc :
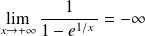 .
.
Donc :
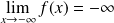 et
et
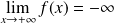 . Et :
. Et :
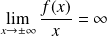 .
.
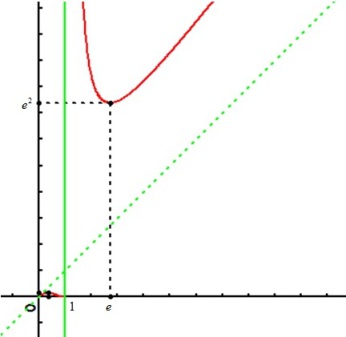
La courbe de
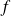 admet en
admet en
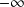 et en
et en
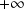 une branche parabolique de direction
une branche parabolique de direction
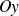 .
.
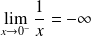 , donc :
, donc :
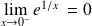 . Donc :
. Donc :
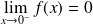 et
et
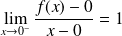 .
.
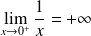 , donc :
, donc :
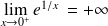 . Donc :
. Donc :
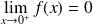 et
et
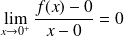 .
.
Donc
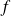 est prolongeable en
est prolongeable en
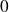 et sa courbe admet un « point limite »
et sa courbe admet un « point limite »
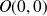 avec une demi-tangente à gauche de pente
avec une demi-tangente à gauche de pente
 et une demi-tangente à droite de pente
et une demi-tangente à droite de pente
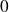 .
.
Par composition, la fonction
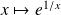 est dérivable sur
est dérivable sur
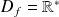 .
.
Donc la fonction
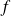 est dérivable sur
est dérivable sur
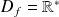 comme quotient de fonctions dérivables.
comme quotient de fonctions dérivables.
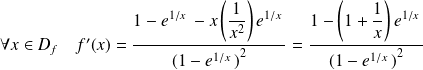 .
.
Donc
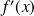 est du signe de
est du signe de
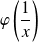 si
si
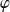 est définie par :
est définie par :
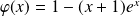 .
.
La fonction
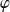 est dérivable sur
est dérivable sur
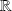 et :
et :
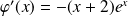 .
.
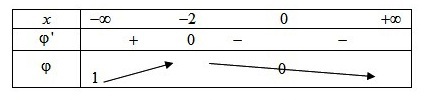
Sur
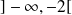 ,
,
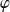 est strictement croissante et
est strictement croissante et
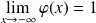 , donc
, donc
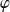 est positive.
est positive.
Sur
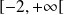 ,
,
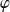 est strictement décroissante et
est strictement décroissante et
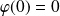 , donc
, donc
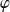 est positive sur
est positive sur
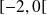 et négative sur
et négative sur
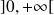 .
.
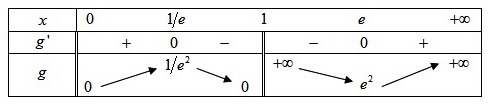
On en déduit le signe de
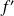 .
.
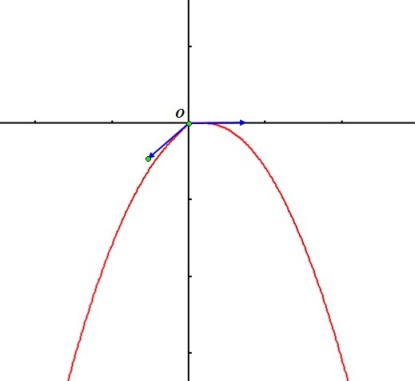
Question
Etudier et représenter graphiquement la fonction définie par :
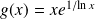 .
.
La fonction
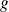 est définie si et seulement si :
est définie si et seulement si :
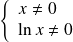 . Donc :
. Donc :
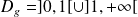 .
.
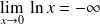 , donc :
, donc :
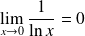 , donc :
, donc :
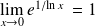 . Donc :
. Donc :
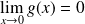 .
.
Donc
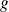 est prolongeable en
est prolongeable en
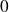 et sa courbe admet un « point limite »
et sa courbe admet un « point limite »
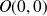 avec une tangente pente
avec une tangente pente
 car :
car :
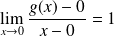 .
.
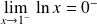 , donc :
, donc :
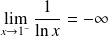 , donc :
, donc :
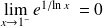 . Donc :
. Donc :
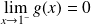 .
.
Et :
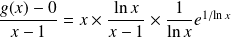 . Or :
. Or :
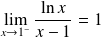 et
et
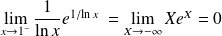 .
.
Donc
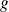 est prolongeable à gauche de
est prolongeable à gauche de
 et sa courbe admet un « point limite »
et sa courbe admet un « point limite »
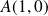 avec une tangente horizontale.
avec une tangente horizontale.
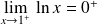 , donc :
, donc :
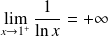 , donc :
, donc :
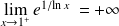 . Donc :
. Donc :
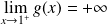 .
.
A droite de
 , la courbe de
, la courbe de
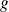 admet une asymptote verticale d'équation
admet une asymptote verticale d'équation
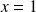 .
.
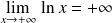 , donc :
, donc :
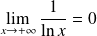 , donc :
, donc :
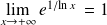 . Donc :
. Donc :
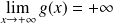 .
.
De plus :
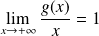 et :
et :
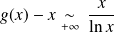 . Donc :
. Donc :
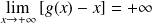 .
.
Donc la courbe de
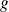 admet en
admet en
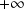 une direction asymptotique
une direction asymptotique
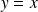 .
.
Par composition, la fonction
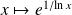 est dérivable sur
est dérivable sur
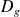 .
.
Donc
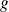 est dérivable sur
est dérivable sur
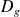 comme produit de fonctions dérivables.
comme produit de fonctions dérivables.
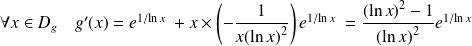 .
.
Donc
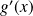 est du signe de :
est du signe de :
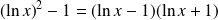 .
.
Question
Etudier et représenter graphiquement la fonction définie par :
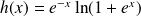 .
.
Pour étudier le sens de variations de
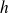 , introduisez une fonction auxiliaire en isolant le logarithme.
, introduisez une fonction auxiliaire en isolant le logarithme.
La fonction
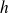 est définie sur
est définie sur
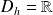 car :
car :
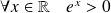 .
.
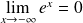 , donc :
, donc :
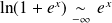 , donc :
, donc :
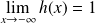 .
.
La courbe de
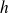 admet en
admet en
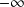 une asymptote horizontale d'équation
une asymptote horizontale d'équation
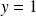 .
.
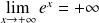 , donc :
, donc :
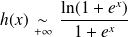 . Or :
. Or :
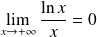 , donc :
, donc :
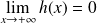 .
.
La courbe de
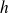 admet en
admet en
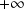 une asymptote horizontale d'équation
une asymptote horizontale d'équation
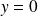 .
.
Par composition, la fonction
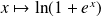 est dérivable sur
est dérivable sur
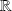 .
.
Donc
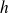 est dérivable sur
est dérivable sur
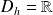 comme produit de fonctions dérivables.
comme produit de fonctions dérivables.
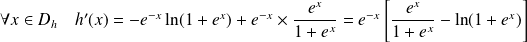 .
.
Donc
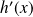 est du signe de
est du signe de
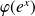 en posant :
en posant :
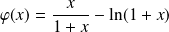 .
.
Il suffit d'étudier la fonction
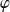 sur
sur
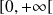 puisque :
puisque :
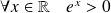 .
.
La fonction
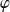 est dérivable et :
est dérivable et :
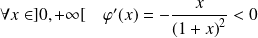 .
.
Donc
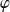 est strictement décroissante sur
est strictement décroissante sur
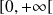 et :
et :
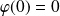 .
.
Donc :
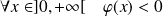 . Donc :
. Donc :
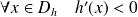 .
.
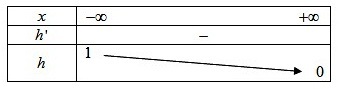
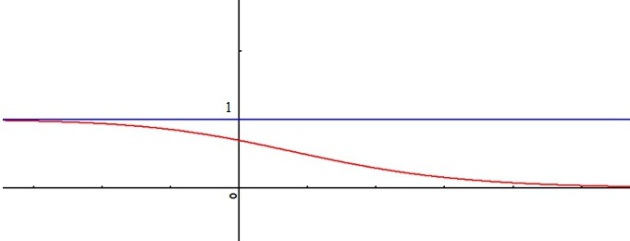
La courbe de
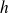 présente un point d'inflexion, mais on ne peut trouver qu'une valeur approchée de son abscisse.
présente un point d'inflexion, mais on ne peut trouver qu'une valeur approchée de son abscisse.