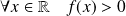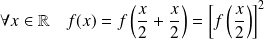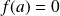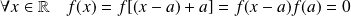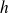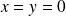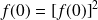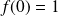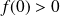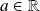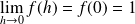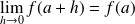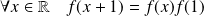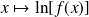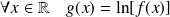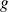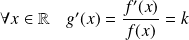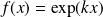Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
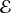 l'ensemble des fonctions définies sur
l'ensemble des fonctions définies sur
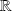 vérifiant :
vérifiant :
 .
.
Soit
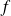 une fonction non nulle appartenant à
une fonction non nulle appartenant à
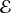 .
.
Question
On suppose maintenant que
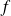 est continue en
est continue en
 .
.
Question
Question
Démontrer que
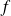 est dérivable sur
est dérivable sur
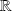 .
.
Exprimez
 à l'aide d'une primitive
à l'aide d'une primitive
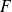 de
de
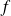 sur
sur
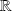 .
.
La fonction
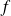 est continue sur
est continue sur
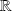 , donc admet une primitive
, donc admet une primitive
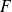 qui s'annule en
qui s'annule en
 .
.
Pour tout réel
 , les fonctions
, les fonctions
 et
et
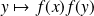 sont continues sur
sont continues sur
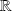 , donc intégrables sur
, donc intégrables sur
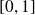 .
.
Et :
 .
.
Or :
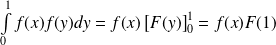 .
.
Et :
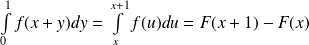 par changement de variable
par changement de variable
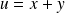 .
.
Donc pour tout réel
 :
:
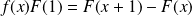 .
.
Or :
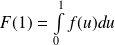 et :
et :
 , donc :
, donc :
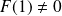 .
.
Donc pour tout réel
 :
:
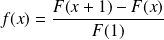 . Or
. Or
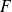 est dérivable sur
est dérivable sur
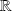 .
.
Conclusion : La fonction
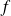 est dérivable sur
est dérivable sur
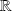 .
.
Question
Question
Réciproquement, soit
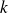 un réel et
un réel et
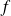 la fonction définie par :
la fonction définie par :
 .
.
Question
Démontrer que la fonction
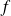 appartient à
appartient à
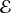 .
.
Utilisez la propriété du logarithme népérien.
La fonction
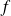 est définie par :
est définie par :
 .
.
La fonction
 est bijective de
est bijective de
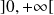 dans
dans
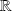 , donc la fonction
, donc la fonction
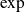 est bijective de
est bijective de
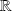 dans
dans
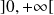 .
.
Donc :
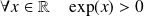 . Donc :
. Donc :
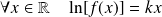 .
.
Donc :
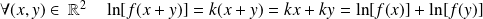 .
.
Donc :
 , donc :
, donc :
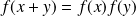 .
.
Conclusion : Toute fonction définie par :
 appartient à
appartient à
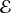 .
.
Question
Soit un réel
 . Démontrer que :
. Démontrer que :
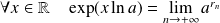 pour toute suite
pour toute suite
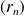 de rationnels convergeant vers
de rationnels convergeant vers
 .
.
Déterminez
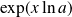 pour
pour
 appartenant successivement à
appartenant successivement à
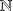 , à
, à
 , à
, à
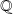 , puis utilisez la continuité de la fonction.
, puis utilisez la continuité de la fonction.
La fonction
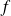 définie par :
définie par :
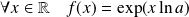 appartient à
appartient à
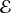 .
.
Donc :
 .
.
On en déduit par une récurrence simple que :
 .
.
Donc :
 .
.
Et :
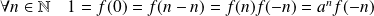 , donc :
, donc :
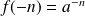 .
.
Donc :
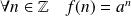 .
.
Tout rationnel
 peut s'écrire sous la forme
peut s'écrire sous la forme
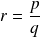 avec
avec
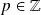 et
et
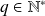 .
.
Donc :
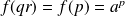 . Or :
. Or :
 . Donc :
. Donc :
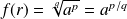 .
.
Donc :
 .
.
La fonction
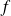 est continue sur
est continue sur
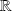 par composition de fonctions continues.
par composition de fonctions continues.
Donc, si
 , alors
, alors
 .
.
Conclusion :
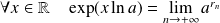 pour toute suite
pour toute suite
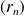 de rationnels convergeant vers
de rationnels convergeant vers
 .
.