Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Etudier et représenter graphiquement la fonction définie par :
.
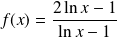La fonction
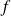est définie si et seulement si :
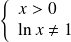, donc :
.
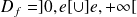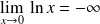, donc :
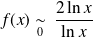, donc :
.
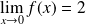Donc
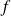est prolongeable par continuité en
.
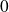La courbe de
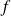admet un « point limite »
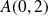avec une tangente verticale car :
.
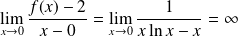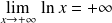, donc :
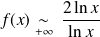, donc :
.
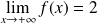La courbe de
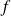admet en
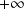une asymptote horizontale d'équation :
.
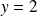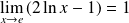et
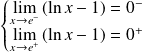. Donc :
.
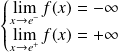La courbe de
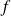admet une asymptote verticale d'équation
.
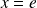La fonction
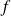est dérivable sur
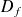comme quotient de fonctions dérivables.
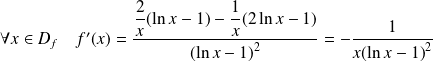, donc :
.
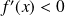Question
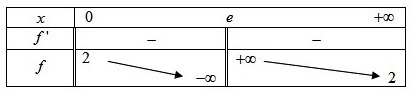
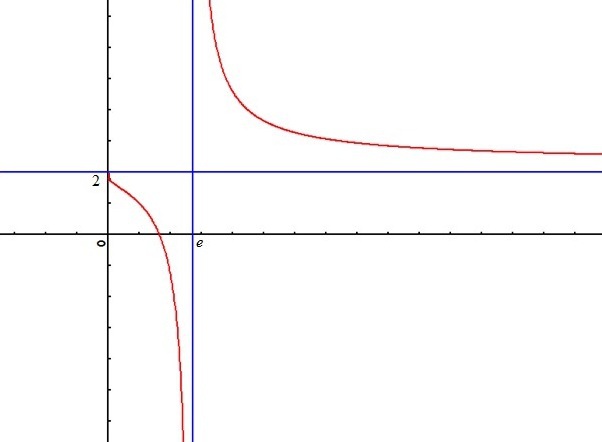
Etudier et représenter graphiquement la fonction définie par :
.
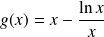Pour étudier le sens de variations de
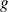, introduisez une fonction auxiliaire.
La fonction
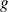est définie si et seulement si :
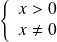, donc :
.
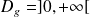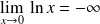et
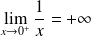, donc :
.
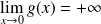La courbe de
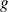admet une asymptote verticale d'équation
.
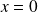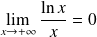, donc :
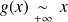, donc :
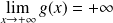et
.
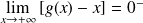La courbe de
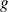admet en
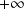une asymptote oblique d'équation
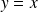et se trouve en dessous de cette asymptote.
La fonction
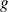est dérivable sur
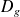comme somme et quotient de fonctions dérivables.
.
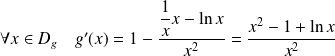Donc
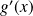est du signe de :
.
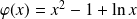La fonction
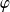est dérivable comme somme de fonctions dérivables.
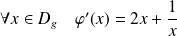, donc :
.
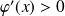Donc la fonction
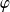est strictement croissante et
.
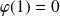Donc :
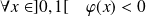et :
.
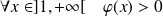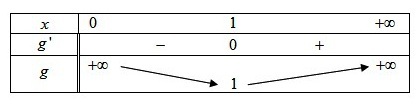
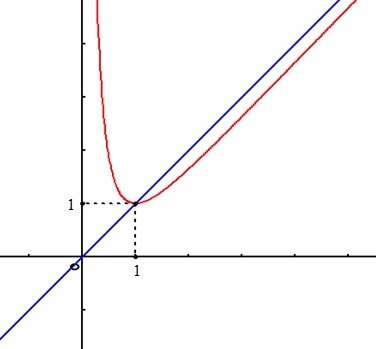
Remarque :
La courbe de
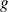se rapproche très lentement de son asymptote et la concavité change sur
.
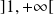En effet :
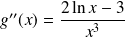. Donc il y a un point d'inflexion d'abscisse
.
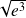Question
Etudier et représenter graphiquement la fonction définie par :
.
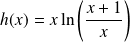Pour étudier le sens de variations de
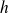, utilisez la dérivée seconde.
La fonction
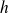est définie si et seulement si :
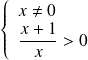, donc :
.
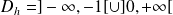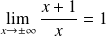, donc :
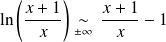, donc :
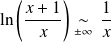, donc :
.
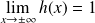La courbe de
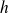adme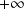t en
et en
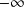une asymptote horizontale d'équation
.
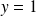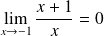, donc :
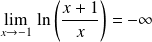, donc :
.
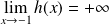La courbe de
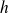admet une asymptote verticale d'équation
.
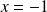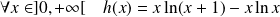. Or :
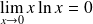. Donc :
.
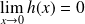Donc
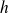est prolongeable par continuité en
.
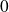La courbe de
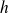admet un « point limite »
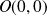avec une tangente verticale car :
.
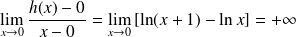La fonction
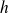est dérivable sur
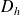par composition et produit de fonctions dérivables.
.
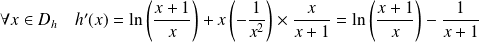La fonction
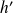est également dérivable sur
.
.
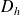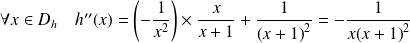Donc :
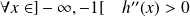et :
.
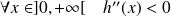Sur
,
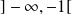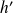est croissante et
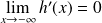, donc :
.
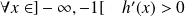Sur
,
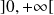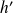est décroissante et
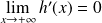, donc :
.
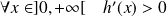