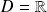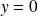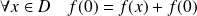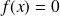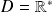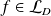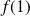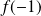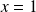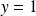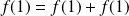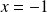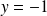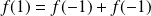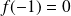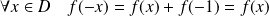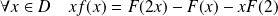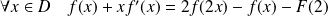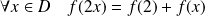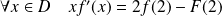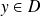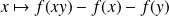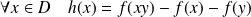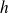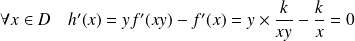Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
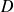 une partie non vide de
une partie non vide de
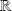 .
.
On note
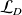 l'ensemble des applications de
l'ensemble des applications de
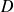 dans
dans
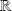 qui vérifient :
qui vérifient :
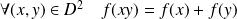 .
.
Question
Question
On suppose maintenant que
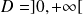 et soit
et soit
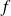 une fonction continue en
une fonction continue en
 qui appartient à
qui appartient à
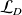 .
.
Question
Démontrer que
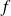 est continue sur
est continue sur
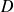 .
.
Pour tout
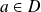 , calculez
, calculez
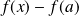 .
.
Soit
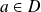 . On a :
. On a :
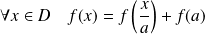 .
.
La fonction
 :
:
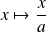 est continue sur
est continue sur
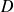 et
et
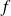 est continue en
est continue en
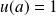 .
.
Donc par composition,
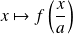 est continue en
est continue en
 , donc
, donc
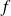 est continue en
est continue en
 .
.
Conclusion : La fonction
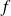 est continue sur
est continue sur
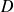 .
.
Remarque :
La conclusion serait la même si l'on supposait la continuité de
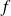 en un autre point que
en un autre point que
 .
.
Question
Démontrer que
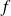 est dérivable sur
est dérivable sur
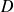 .
.
Exprimez
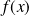 à l'aide d'une primitive
à l'aide d'une primitive
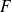 de
de
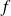 sur
sur
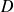 .
.
La fonction
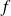 est continue sur
est continue sur
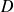 , donc elle possède une unique primitive
, donc elle possède une unique primitive
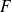 sur
sur
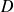 qui s'annule en
qui s'annule en
 .
.
Pour tout
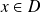 , les fonctions
, les fonctions
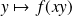 et
et
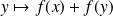 sont continues sur
sont continues sur
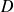 .
.
Elles sont donc intégrables sur
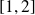 et :
et :
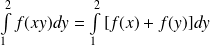 .
.
Or :
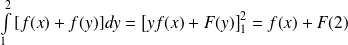 .
.
Et :
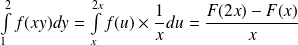 par changement de variable
par changement de variable
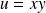 .
.
Donc pour tout
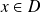 , on a :
, on a :
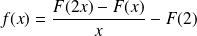 .
.
Or la fonction
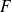 est dérivable sur
est dérivable sur
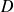 .
.
Conclusion : La fonction
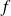 est dérivable sur
est dérivable sur
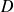 .
.
Question
Réciproquement, soit
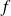 une fonction dérivable sur
une fonction dérivable sur
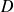 vérifiant
vérifiant
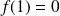 et pour laquelle il existe un réel
et pour laquelle il existe un réel
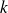 tel que :
tel que :
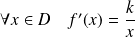 .
.