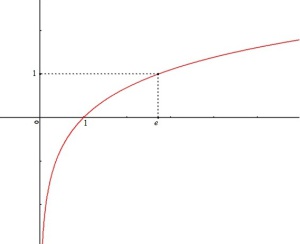
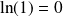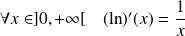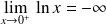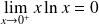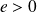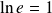Fonctions logarithmes
Définition :
On appelle fonction logarithme toute fonction non nulle, continue sur
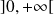et qui vérifie :
.
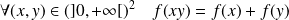On peut remarquer qu'il suffit de supposer la continuité en un point (par exemple en
) pour avoir la continuité sur
.
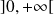Fondamental :
Propriétés :
Toute fonction logarithme vérifie :
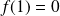.Toute fonction logarithme est dérivable sur
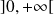.Pour toute fonction logarithme, il existe un réel
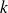non nul tel que :
.
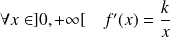Or la fonction
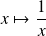est continue sur
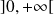, donc admet une primitive.
Définition :
On appelle logarithme népérien, noté
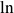, l'unique primitive sur
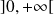de la fonction
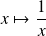qui s'annule en
.
Fondamental :
Propriétés
|  |
La fonction
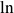est une fonction logarithme.
Fondamental :
Propriétés algébriques
.
.
.
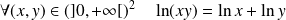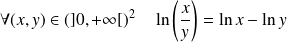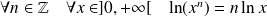Si
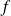est une fonction logarithme, il existe un réel non nul
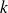tel que :
.
Donc la fonction
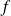est bijective de
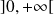dans
.
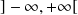Donc il existe un unique réel strictement positif
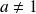tel que :
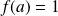, donc :
.
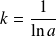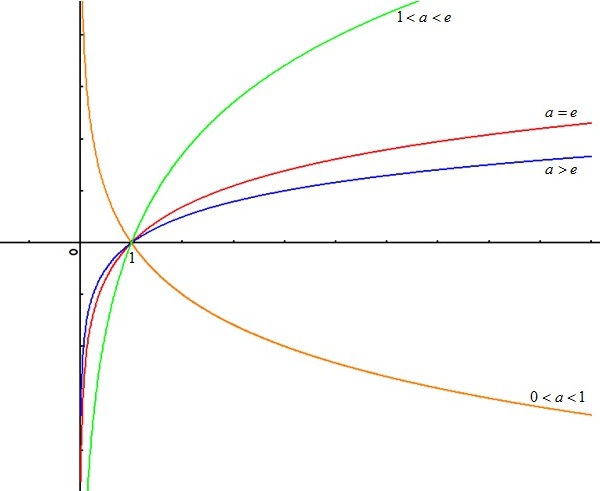
Définition :
Si
est un réel strictement positif, différent de
, la fonction logarithme de base
est définie par :
.
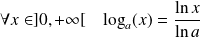Le logarithme népérien est le logarithme de base
.
