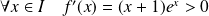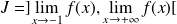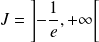Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
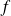 la fonction définie par :
la fonction définie par :
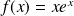 .
.
Question
Question
Déterminer le
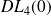 de la fonction réciproque de
de la fonction réciproque de
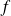 .
.
Partant de la forme du
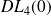 de
de
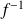 , calculez celui de
, calculez celui de
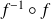 , puis utilisez l'unicité.
, puis utilisez l'unicité.
On peut remarquer que :
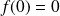 . Donc :
. Donc :
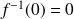 .
.
La dérivée de
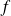 ne s'annule pas sur
ne s'annule pas sur
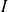 , donc
, donc
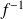 est dérivable sur
est dérivable sur
 :
:
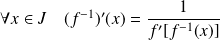 .
.
Donc
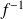 est de classe
est de classe
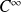 sur
sur
 , donc elle admet un
, donc elle admet un
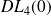 .
.
Il est de la forme :
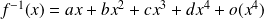 car :
car :
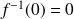 .
.
On peut composer avec le
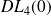 de
de
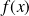 puisque :
puisque :
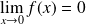 .
.
Donc :
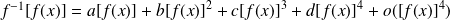 .
.
Or :
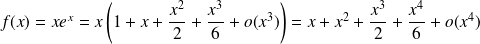 .
.
Donc :
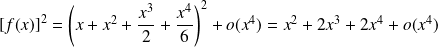 .
.
De même :
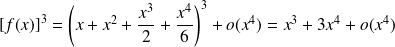 .
.
Et :
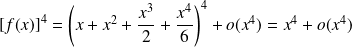 .
.
Donc :
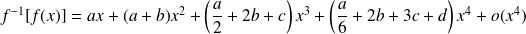 .
.
Or :
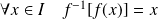 .
.
Donc par unicité du
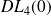 , on a :
, on a :
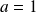 et
et
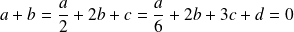 .
.
Donc :
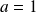 ,
,
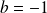 ,
,
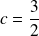 et
et
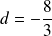 .
.
Conclusion :
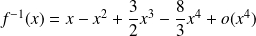 .
.