Développements limités
L'approximation locale d'une fonction par un polynôme permet par exemple de calculer des limites.
Définition :
Une fonction
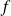 admet un développement limité d'ordre
admet un développement limité d'ordre
 en
en
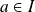 , noté
, noté
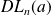 , s'il existe un polynôme
, s'il existe un polynôme
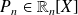 tel que :
tel que :
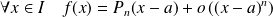 .
.
S'il existe, le polynôme
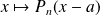 est unique : c'est la partie régulière du
est unique : c'est la partie régulière du
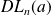 .
.
Par changement de variable
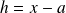 , on se ramène à un développement limité en
, on se ramène à un développement limité en
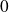 .
.
Fondamental :
Propriétés
Si la fonction
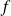 admet un
admet un
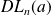 , il est unique.
, il est unique.Si la fonction
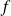 admet un
admet un
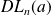 , elle admet en
, elle admet en
 des développements limités de tout ordre
des développements limités de tout ordre
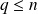 .
.Leur partie régulière est obtenue en tronquant le polynôme
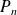 à l'ordre
à l'ordre
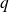 :
:
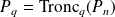 .
. Si la fonction
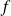 admet un
admet un
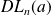 et si
et si
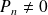 , alors :
, alors :
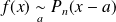 .
.
La formule de Taylor-Young permet de trouver des développements limités d'ordre
 des fonctions de classe
des fonctions de classe
 .
.
Fondamental :
Développements limités usuels en 0
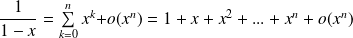 .
.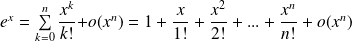 .
.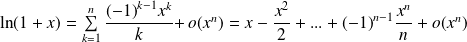 .
.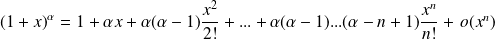 .
.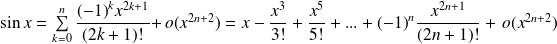 .
.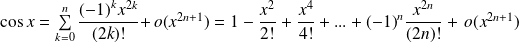 .
.
Par opérations sur ces développements limités, on en déduit ceux des autres fonctions.
Fondamental :
Opérations algébriques
Soient
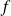 et
et
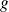 deux fonctions qui admettent des
deux fonctions qui admettent des
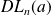 de parties régulières
de parties régulières
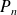 et
et
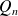 .
.
Si
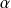 et
et
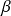 sont des réels, alors la fonction
sont des réels, alors la fonction
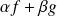 admet un
admet un
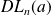 dont la partie régulière est
dont la partie régulière est
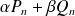 .
.La fonction
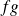 admet un
admet un
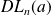 dont la partie régulière est
dont la partie régulière est
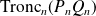 .
.
Composition
Si la fonction
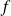 admet un
admet un
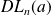 , si
, si
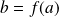 et si la fonction
et si la fonction
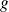 admet un
admet un
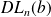 , alors la fonction
, alors la fonction
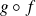 admet un
admet un
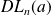 de partie régulière
de partie régulière
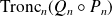 .
.
Pour déterminer le développement limité d'un quotient, on compose le dénominateur avec la fonction
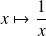 , puis l'on effectue le produit avec le numérateur.
, puis l'on effectue le produit avec le numérateur.
Fondamental :
Intégration
Si la fonction
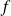 est continue sur un intervalle
est continue sur un intervalle
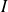 contenant
contenant
 et si
et si
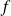 admet un
admet un
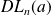 de partie régulière
de partie régulière
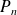 , toute primitive
, toute primitive
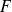 de
de
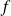 sur
sur
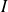 admet un
admet un
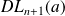 dont la partie régulière est la primitive de
dont la partie régulière est la primitive de
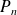 qui prend la valeur
qui prend la valeur
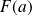 en
en
 .
.
Par contre, une fonction peut admettre un développement limité sans que sa dérivée en admette un.





