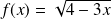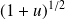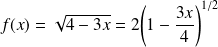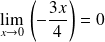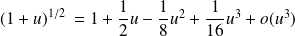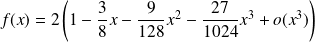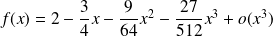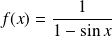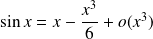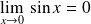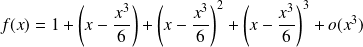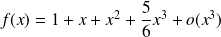Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Déterminer le
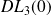de :
.
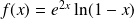Utilisez la composition et le produit des développements limités usuels.
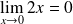et au voisinage de
:
.
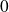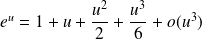Donc, par composition :
.
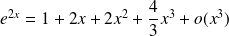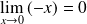et au voisinage de
:
.
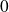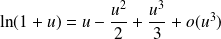Donc, par composition :
.
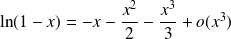Donc :
.
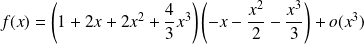Dans le produit, on ne conserve que les termes de degré inférieur ou égal à
.
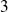Conclusion :
.
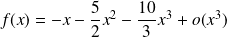Question
Question
Déterminer le
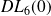de :
.
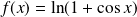N'oubliez pas que les développements limités usuels sont au voisinage de
!
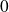Transformez les expressions pour vous y ramener.
On peut remarquer que :
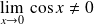, donc on transforme l'expression.
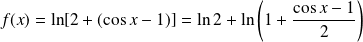. On pose :
.
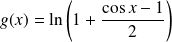Au voisinage de
:
.
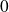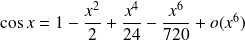Donc, au voisinage de
:
.
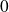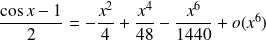et au voisinage de 0 :
.
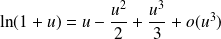Remarque :
Comme le développement de
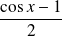commence à
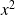, l'ordre
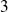suffit pour le logarithme.
Donc :
.
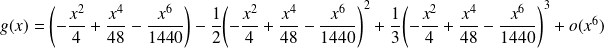On ne conserve que les termes de degré inférieur ou égal à
.
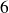Donc :
.
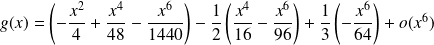Conclusion :
.
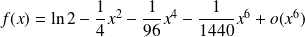Question
Question
Déterminer le
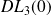de :
.
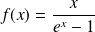Choisissez bien l'ordre du développement limité de
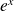car il y aura une simplification de la fraction.
Au voisinage de
:
.
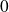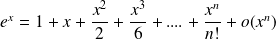Donc :
.
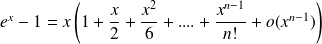Dans l'expression de
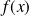, il y aura donc une simplification par
.
Donc, pour avoir un
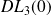de
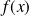, il faut prendre un
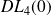de
.
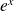Au voisinage de
:
.
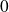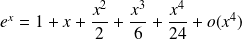Donc :
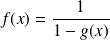avec :
.
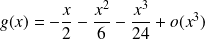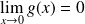et au voisinage de
:
.
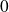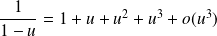Donc :
.
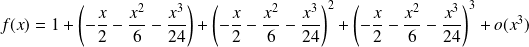On ne conserve que les termes de degré inférieur ou égal à
.
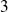Conclusion :
.
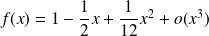