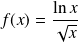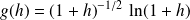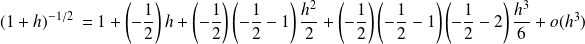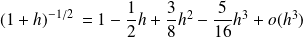Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Déterminer le
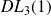 de :
de :
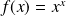 .
.
Utilisez la forme exponentielle, et posez :
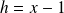 pour vous ramener à un développement limité en
pour vous ramener à un développement limité en
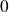 .
.
On pose :
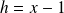 . Donc :
. Donc :
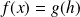 avec :
avec :
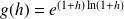 .
.
Au voisinage de
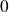 :
:
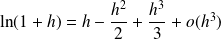 .
.
Donc :
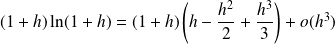 .
.
On ne conserve que les termes de degré inférieur ou égal à
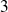 .
.
Donc :
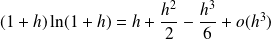 .
.
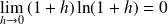 et au voisinage de
et au voisinage de
 :
:
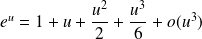 .
.
Donc :
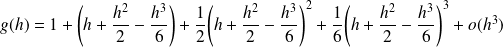 .
.
On ne conserve que les termes de degré inférieur ou égal à
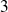 .
.
Donc :
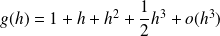 au voisinage de
au voisinage de
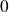 .
.
Conclusion :
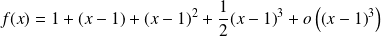 au voisinage de
au voisinage de
 .
.
Question
Question
Déterminer le
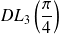 de :
de :
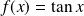 .
.
Posez :
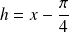 pour vous ramener à un développement limité en
pour vous ramener à un développement limité en
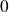 .
.
On pose :
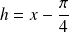 . Donc :
. Donc :
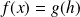 avec :
avec :
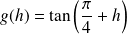 .
.
Donc :
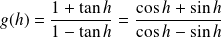 .
.
Au voisinage de
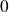 :
:
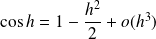 et :
et :
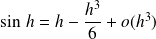 .
.
Donc :
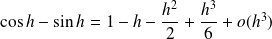 et :
et :
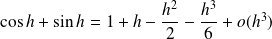 .
.
Donc :
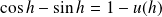 avec :
avec :
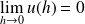 .
.
Or , au voisinage de
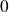 :
:
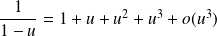 .
.
Donc :
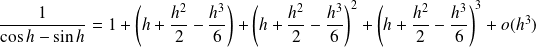 .
.
On ne conserve que les termes de degré inférieur ou égal à
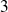 .
.
Donc :
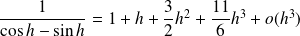 .
.
Donc :
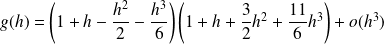 .
.
On ne conserve que les termes de degré inférieur ou égal à
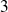 .
.
Donc :
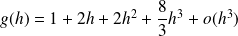 au voisinage de
au voisinage de
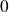 .
.
Conclusion :
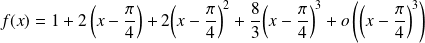 au voisinage de
au voisinage de
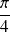 .
.