Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Démontrer que :
.
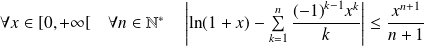Utilisez l'inégalité de Taylor-Lagrange[1].
La fonction
:
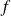est de classe
sur
.
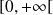Et :
,
,
, ...
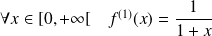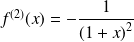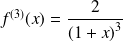Une récurrence simple montre que :
.
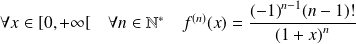Donc :
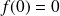et
.
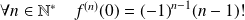De plus :
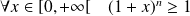, donc :
.
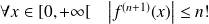On applique l'inégalité de Taylor-Lagrange à l'ordre
entre
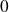et
.
Conclusion :
.
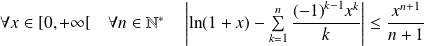Question
En déduire la convergence de la série
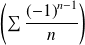et sa somme.
Pour
:
.
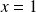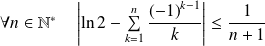Donc :
.
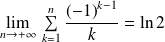Conclusion : La série
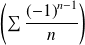est convergente et sa somme est
.
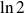Question
En déduire une valeur approchée de
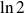à
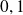près.
Choisissez
pour que l'encadrement précédent donne une valeur approchée à
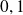près.
Pour que
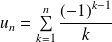soit une valeur approchée de
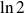à
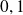près, il suffit que
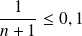, donc il suffit que
.
Or :
.
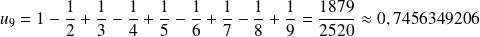L'inégalité donne :
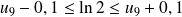. Donc :
.
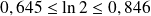On ne peut pas en déduire une valeur décimale approchée à
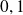près.
Pour
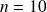, on obtient :
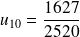et :
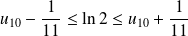. Donc :
.
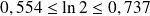Donc, en comparant les deux inégalités :
.
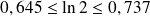Conclusion : Une valeur décimale approchée de
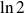à
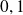près est :
.
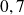Remarque :
La convergence de la série est beaucoup plus lente que pour l'exponentielle.
