Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
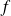une fonction de classe
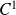sur un intervalle ouvert
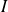, et soit
.
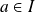Question
Déterminer la limite en
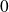de
.
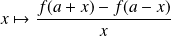Utilisez la formule de Taylor-Young[1].
La fonction
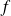est de classe
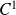sur
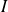, donc on peut lui appliquer la formule de Taylor-Young à l'ordre
.
Donc :
.
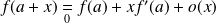Et :
.
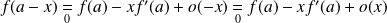Donc :
.
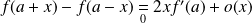Donc :
.
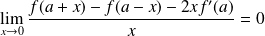Conclusion :
.
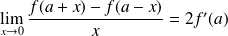On suppose que
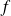est de classe
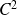sur
.
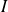Question
Calculer la limite
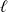de
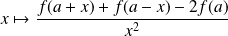en
.
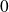Utilisez la formule de Taylor-Young[1].
La fonction
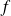est de classe
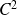sur
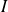, donc on peut lui appliquer la formule de Taylor-Young à l'ordre
.
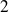Donc :
.
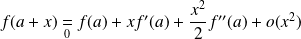Et :
.
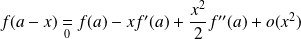Donc :
.
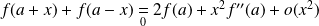Donc :
.
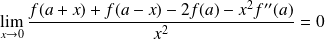Conclusion :
.
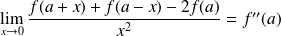On suppose que
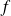est de classe
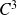sur
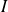et que :
.
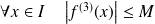Question
Démontrer que :
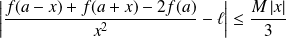si
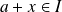et
.
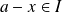Utilisez l'inégalité de Taylor-Lagrange[2].
La fonction
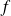est de classe
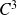sur
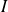et
.
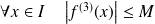Donc on peut appliquer l'inégalité de Taylor-Lagrange à l'ordre
.
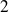Donc, si
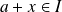, on a :
.
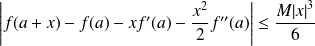Et, si
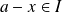, on a :
.
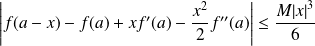Or :
.
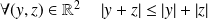Donc :
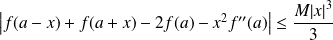si
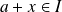et
.
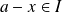Conclusion :
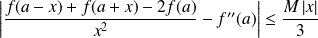si
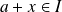et
.
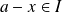