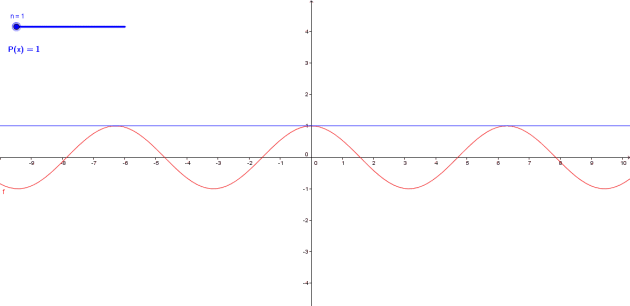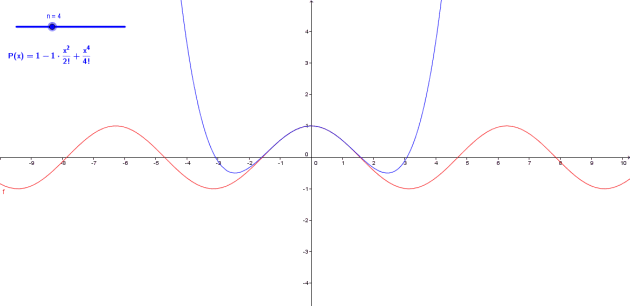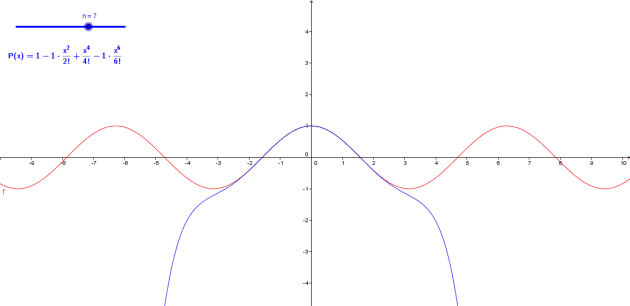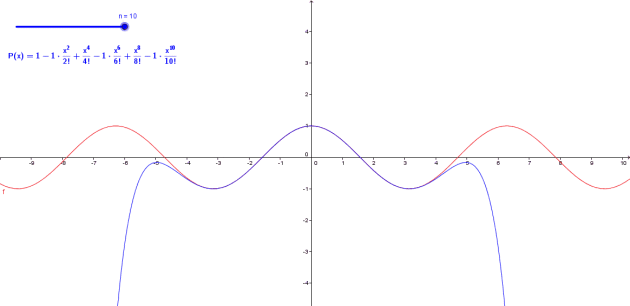
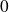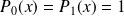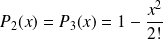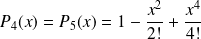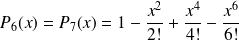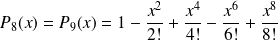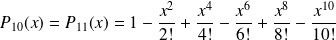Formules de Taylor
Soit
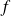une fonction définie sur un intervalle
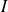de
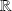et à valeurs réelles.
L'objectif est d'approcher la fonction
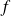par un polynôme.
Définition :
Si la fonction
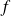est dérivable
fois sur l'intervalle
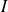et si
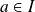, on appelle polynôme de Taylor de la fonction
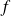à l'ordre
en
le polynôme
.
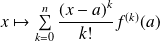Si l'on connaît la valeur du polynôme de Taylor de
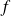en un point
, on peut exprimer la valeur de
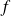sous plusieurs formes.
Fondamental :
Formule de Taylor avec reste intégral
Si
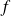est de classe
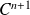sur
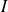, alors pour tous
et
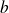de
:
.
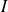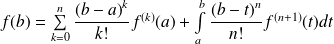Mais en général, on ne sait pas calculer cette intégrale.
Fondamental :
Formule de Taylor-Lagrange
Si
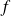est de classe
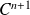sur
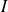, alors pour tous
et
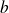(distincts) de
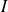, il existe
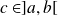tel que :
.
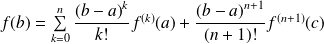C'est une généralisation de l'égalité des accroissements finis. On connaît l'existence de
, mais pas son calcul.
Dans certains cas, on peut trouver une majoration.
Fondamental :
Inégalité de Taylor-Lagrange
Si
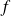est de classe
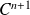sur
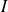et si
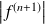est majorée par
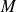, alors :
.
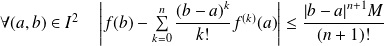Cette inégalité, ainsi que la formule qui suit sont valables aussi pour les fonctions à valeurs complexes.
Fondamental :
Formule de Taylor-Young
Si la fonction
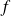est de classe
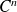sur un intervalle
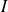, alors pour tout
:
.
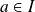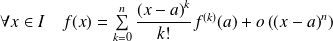Cette formule est une formule « locale » : elle donne une approximation de
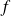par son polynôme de Taylor au voisinage de
.
Exemple :
Par exemple, pour la fonction cosinus au voisinage de
:
.
.
.
.
.
.
Lorsque
augmente, la courbe du polynôme de Taylor d'ordre
est de plus en plus proche de la courbe du cosinus au voisinage de
.
