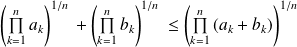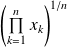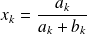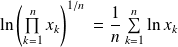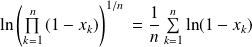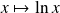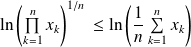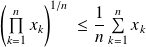Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
, ...,
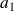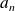et
, ...,
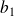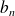des réels strictement positifs.
Question
Question
Démontrer que :
.
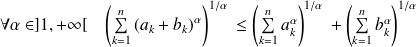Ramenez le problème posé à la minoration de deux termes de la forme
.
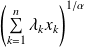Utilisez la convexité.
L'inégalité à démontrer peut s'écrire :
.
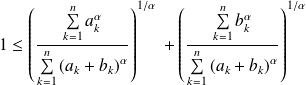Ou encore :
.
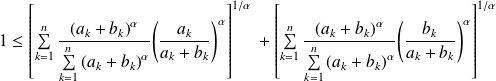On pose :
, et donc :
.
L'inégalité à démontrer s'écrit donc :
.
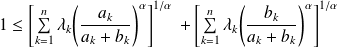La fonction
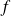définie par :
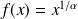est dérivable deux fois sur
.
Et :
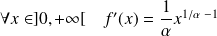, donc :
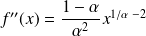, donc :
.
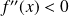Donc la fonction
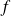est concave sur
.
Donc :
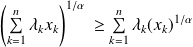pour toute famille
de
.
Donc :
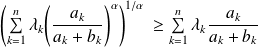et
.
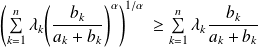Donc :
.
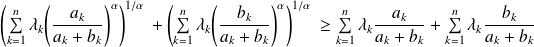Donc :
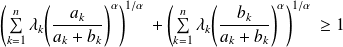car
.
Conclusion :
.
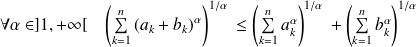